Question

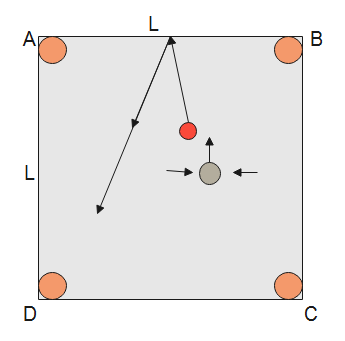
In a game of carrom board, the Queen (a wooden disc of radius 2cm and mass 50gm) is placed at the exact center of the horizontal board. The striker is a smooth plastic disc of radius 3cm and mass 100gm. The board is frictionless. The striker is given an initial velocity 'u' parallel to the sides BC and AD so that it hits the Queen inelastically with coefficient of restitution=2/3. The impact parameter for the collision is’d’ (as shown in the figure). The Queen rebounds from the edge AB of the board inelastically with the same coefficient of restitution=2/3 and enters the hole D following the dotted path as shown. The side of the board is L. Find the value of impact parameter ‘d’ and the time which the Queen takes to enter hole D after collision with the striker:

Answer 1

In this question, we will use the basic trigonometry to solve the values; here we use the formula to find the impact parameter and the law of conservation of momentum. This will help us to get the required result. Further, we will study the basics of collision, for our better understanding.

Formula used:
$d = 5\sin \alpha$
$mu\cos \alpha = m{u_2} + m{u_1}$

Complete answer:
Let us assume O be the point where the queen strikes on AD after collision. Also, the velocity of queen after collision is ${V_x} + {V_y}$ with ${V_x}$ along the x-axis and ${V_y}$ along the y-axis.
So, after collision from edge AB,${V_x}$remains same, velocity in y direction becomes $\dfrac{{2{V_y}}}{3}$
$\dfrac{{\tan \alpha }}{{\tan \beta }} = \dfrac{{\dfrac{{{V_x}}}{{{V_y}}}}}{{\dfrac{{3{V_x}}}{{2{V_y}}}}} = \dfrac{2}{3}$
Now, by using the basic trigonometry we get:
$\dfrac{L}{2} = \dfrac{L}{2}\tan \alpha + L\tan \theta$
Now, by substituting the values and solving, we get:
$\dfrac{1}{2} = \dfrac{1}{2}\tan \alpha + \dfrac{3}{2}\tan \alpha$
$\Rightarrow \tan \alpha = \dfrac{1}{4}$
$\cos \alpha = \dfrac{4}{{\sqrt {17} }}$
Now, the impact parameter is given by:
$d = 5\sin \alpha = \dfrac{5}{{\sqrt {17} }}cm$
Now conservation of momentum along the line of collision
$2mu\cos \alpha = m{u_2} + 2m{u_1}............(1)$
Here, 2m is equal to 100g, it is the mass of the striker and m is 50g, it is the mass of the queen, u is the velocity of the striker before collision, ${u_2}$ is the velocity of the queen along the collision line and ${u_1}$​ is the velocity of striker after collision along the line of collision.
Here, from coefficient of restitution equation we get:
$\dfrac{2}{3} = \dfrac{{{u_2} - {u_1}}}{u}.........(2)$
Now, from equation (1) and (2), we get:
\eqalign{ & time = \dfrac{{\dfrac{L}{2}}}{{{u_2}\sin \alpha }} \cr & \therefore time = \dfrac{{153L}}{{30u}} \cr}
Therefore, we get the required impact parameter and the time the Queen takes to enter hole D after collision with the striker.

Additional information:
From the law of conservation of mass which says that mass can neither be created nor destroyed in any chemical reactions. Also, it can be defined as the mass of any one element at the beginning of a reaction will equal the mass of that element at the end of the reaction.
We know that collision means when two objects come in contact with each other for a very short period. Collision is an interaction between two masses for a very short interval where the momentum and energy of the colliding masses changes. Here are two types of collision: first is elastic collision where the energy remains the same after interaction or collision and second is inelastic collision where the final energy changes after the collision of the particles or body.

Note:
The resulting mass, energy or velocity after the collision of two particles depends on its direction and magnitude as well. During the solution, one should see that laws of conservation are not violated, i.e., mass can neither be created nor be destroyed and similarly for energy of the particles as well.