Question

In a function$2f(x) + xf(\dfrac{1}{x}) - 2f\left[ {\left| {\sqrt 2 \sin (\pi (x + \dfrac{1}{4}))} \right|} \right] = 4{\cos ^2}\dfrac{{\pi x}}{2} + x\cos \dfrac{\pi }{x}$. Prove that
(i) $f(2) + f(\dfrac{1}{2}) = 1$
(ii) $f(2) + f(1) = 0$

Answer 1

Here we substitute the values of x as 2 in the whole equation and use the quadrant diagram to find the value of the term inside the modulus. Again substituting the value of x as 1 in the equation we get the value of $f(1)$ which we substitute in the equation formed earlier and get our result. For the second part we substitute the value of x as $\dfrac{1}{2}$ and solve.

Complete step-by-step answer:
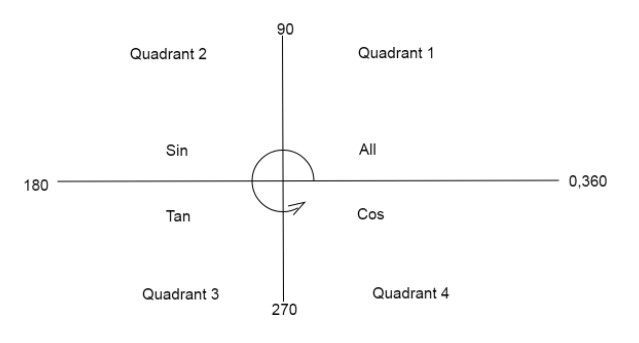
Quadrant diagram helps us to find the value of a trigonometric function when we reduce or add a value to the angle.

We are given the equation in $f(x)$ as:
$2f(x) + xf(\dfrac{1}{x}) - 2f\left[ {\left| {\sqrt 2 \sin (\pi (x + \dfrac{1}{4}))} \right|} \right] = 4{\cos ^2}\dfrac{{\pi x}}{2} + x\cos \dfrac{\pi }{x} …..… (1)$
(i)
First we substitute the value of $x = 2$ in equation (1)
$\Rightarrow 2f(2) + 2f(\dfrac{1}{2}) - 2f\left[ {\left| {\sqrt 2 \sin (\pi (2 + \dfrac{1}{4}))} \right|} \right] = 4{\cos ^2}\dfrac{{2\pi }}{2} + 2\cos \dfrac{\pi }{2}$
Cancel the same values from the numerator and denominator and substitute the value of $\cos \dfrac{\pi }{2} = 0$ in RHS.
$\Rightarrow 2f(2) + 2f(\dfrac{1}{2}) - 2f\left[ {\left| {\sqrt 2 \sin (2\pi + \dfrac{\pi }{4})} \right|} \right] = 4{\cos ^2}\pi + 2 \times 0$
From the quadrant diagram we have $\sin (2\pi + \theta ) = \sin \theta$.
Substitute the value of $\sin (2\pi + \dfrac{\pi }{4}) = \sin \dfrac{\pi }{4} = \dfrac{1}{{\sqrt 2 }}$in LHS and value of $\cos \pi = - 1$
$\Rightarrow 2f(2) + 2f(\dfrac{1}{2}) - 2f\left[ {\left| {\sqrt 2 \times \dfrac{1}{{\sqrt 2 }}} \right|} \right] = 4{( - 1)^2}$
$\Rightarrow 2f(2) + 2f(\dfrac{1}{2}) - 2f(1) = 4$
Divide both sides by 2
$\Rightarrow \dfrac{{2f(2) + 2f(\dfrac{1}{2}) - 2f(1)}}{2} = \dfrac{4}{2}$
Cancel the same terms from numerator and denominator.
$\Rightarrow f(2) + f(\dfrac{1}{2}) - f(1) = 2 ……….… (2)$
Now we find the value of $f(1)$ by substituting the value of $x = 1$ in equation (1)
$\Rightarrow 2f(1) + 1 \times f(\dfrac{1}{1}) - 2f\left[ {\left| {\sqrt 2 \sin (\pi (1 + \dfrac{1}{4}))} \right|} \right] = 4{\cos ^2}\dfrac{{\pi \times 1}}{2} + 1 \times \cos \dfrac{\pi }{1}$
$\Rightarrow 2f(1) + f(1) - 2f\left[ {\left| {\sqrt 2 \sin (\pi + \dfrac{\pi }{4})} \right|} \right] = 4{\cos ^2}\dfrac{\pi }{2} + \cos \pi$
Substitute the value of $\cos \dfrac{\pi }{2} = 0$ and $\cos \pi = - 1$ in RHS
$\Rightarrow 2f(1) + f(1) - 2f\left[ {\left| {\sqrt 2 \sin (\pi + \dfrac{\pi }{4})} \right|} \right] = 4{(0)^2} + ( - 1)$
Using the quadrant diagram we can write $\sin (\pi + \dfrac{\pi }{4}) = - \sin \dfrac{\pi }{4} = - \dfrac{1}{{\sqrt 2 }}$in LHS
$\Rightarrow 2f(1) + f(1) - 2f\left[ {\left| {\sqrt 2 \times \dfrac{{ - 1}}{{\sqrt 2 }}} \right|} \right] = - 1$
Modulus removes the negative sign of the value in LHS
$\Rightarrow 2f(1) + f(1) - 2f(1) = - 1$
Add the values on LHS of the equation
$\Rightarrow f(1) = - 1 ……... … (3)$
Substitute the value of $f(1) = - 1$from equation (3) in equation (2)
$\Rightarrow f(2) + f(\dfrac{1}{2}) - ( - 1) = 2$
$\Rightarrow f(2) + f(\dfrac{1}{2}) + 1 = 2$
Shift the constant value to RHS
$\Rightarrow f(2) + f(\dfrac{1}{2}) = 2 - 1$
$\Rightarrow f(2) + f(\dfrac{1}{2}) = 1$
Hence part (i) proved
(ii)
We substitute the value of $x = \dfrac{1}{2}$ in equation (1)
$\Rightarrow 2f(\dfrac{1}{2}) + \dfrac{1}{2}f(\dfrac{1}{{\dfrac{1}{2}}}) - 2f\left[ {\left| {\sqrt 2 \sin (\pi (\dfrac{1}{2} + \dfrac{1}{4}))} \right|} \right] = 4{\cos ^2}\dfrac{{\pi \dfrac{1}{2}}}{2} + \dfrac{1}{2}\cos \dfrac{\pi }{{\dfrac{1}{2}}}$
$\Rightarrow 2f(\dfrac{1}{2}) + \dfrac{1}{2}f(2) - 2f\left[ {\left| {\sqrt 2 \sin (\dfrac{\pi }{2} + \dfrac{\pi }{4})} \right|} \right] = 4{\cos ^2}\dfrac{\pi }{4} + \dfrac{1}{2}\cos 2\pi$
Using the quadrant diagram we can write $\sin (\dfrac{\pi }{2} + \dfrac{\pi }{4}) = \sin \dfrac{\pi }{4} = \dfrac{1}{{\sqrt 2 }}$in LHS. Substitute$\cos \dfrac{\pi }{4} = \dfrac{1}{{\sqrt 2 }},\cos 2\pi = 1$.
$\Rightarrow 2f(\dfrac{1}{2}) + \dfrac{1}{2}f(2) - 2f\left[ {\left| {\sqrt 2 \times \dfrac{1}{{\sqrt 2 }}} \right|} \right] = 4{(\dfrac{1}{{\sqrt 2 }})^2} + \dfrac{1}{2}(1)$
$\Rightarrow 2f(\dfrac{1}{2}) + \dfrac{1}{2}f(2) - 2f(1) = 4 \times \dfrac{1}{2} + \dfrac{1}{2}$
Substitute the value of $f(1) = - 1$ in LHS.
$\Rightarrow 2f(\dfrac{1}{2}) + \dfrac{1}{2}f(2) - 2( - 1) = 2 + \dfrac{1}{2}$
$\Rightarrow 2f(\dfrac{1}{2}) + \dfrac{1}{2}f(2) + 2 = 2 + \dfrac{1}{2}$
Shift constant from LHS to RHS
$\Rightarrow 2f(\dfrac{1}{2}) + \dfrac{1}{2}f(2) = 2 + \dfrac{1}{2} - 2$
$\Rightarrow 2f(\dfrac{1}{2}) + \dfrac{1}{2}f(2) = \dfrac{1}{2}$
Take LCM on LHS
$\Rightarrow \dfrac{{4f(\dfrac{1}{2}) + f(2)}}{2} = \dfrac{1}{2}$
Cancel the same denominator from both sides of the equation.
$\Rightarrow 4f(\dfrac{1}{2}) + f(2) = 1 ……..… (4)$
We know from part (i) that $f(2) + f(\dfrac{1}{2}) = 1$
Shifting the value of $f(2)$ from LHS to RHS
$\Rightarrow f(\dfrac{1}{2}) = 1 - f(2)$
Substitute this value in equation (4)
$\Rightarrow 4(1 - f(2)) + f(2) = 1$
$\Rightarrow 4 - 4f(2) + f(2) = 1$
Shift constant terms to one side of the equation.
$\Rightarrow - 3f(2) = 1 - 4$
$\Rightarrow - 3f(2) = - 3$
Cancel same terms from both sides
$\Rightarrow f(2) = 1 ……….… (5)$
Add equation (3) and (5)
$f(1) + f(2) = - 1 + 1$
$f(1) + f(2) = 0$
Hence proved

Note: Students many times make the mistake of writing the values of trigonometric terms after the breaking of the angle. Keep in mind to find the values from the quadrant diagram we move in an anticlockwise direction and check if the sign of that function is positive or negative in the quadrant.