Question

In a flight $50$ people speak Hindi, $20$ speak English and $10$ speak both English and Hindi. The number of people who speak at least one of the two languages is
(A) $40$
(B) $50$
(C) $20$
(D) $60$

Answer 1

In this question, we have to find the number of people who can speak in at least any of the languages. Here from the given we assign numbers to the required values and then apply the general Venn diagram formula to find the required result.

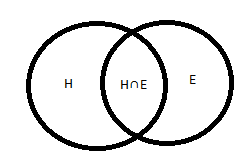
Here, $H \cap E$ means the portion common in H and E.

Complete step-by-step answer:
It is given that, in a flight $50$ people speak Hindi, $20$ speak English and $10$ speak both English and Hindi.
We need to find out the number of people who can speak at least one of the two languages.
We will solve this by Venn diagram.
Here in the above diagram H represents the number of people who can speak in Hindi and E represents the number of people who can speak in English.
Now let us consider,
$n\left( H \right)$=The number of people in the flight can speak in Hindi=$50$.
$n\left( E \right)$= The number of people in the flight can speak in English=$20$
$n(H \cap E)$= The number of people in the flight can speak in both English and Hindi = $10$
We know from the basic formulas for Venn diagrams of two elements
$n(H \cup E) = n\left( H \right) + n\left( E \right) - {\rm{ }}n(H \cap E)$
Here $n(H \cup E)$ is the number of people who speak at least one language.
That is the number of people who can speak at least one of the two languages $= 50 + 20 - 10 = 60$
Hence there are 60 people who can speak at least one of the two languages.

Hence, (D) is the correct option.

Note: This question can be explained in a simple way that we should find the number of people who could speak at least one of the languages for that we should add the number of people who speak the languages individually and then subtract the number of people who speak both the languages. In simple if ‘x’, ‘y’ is the number of people speak the languages separately and ‘z’ be the number of people who speak both the languages then the number of people who speak at least one language ‘o’ is given by the formula $o = x + y - z$.