Question

In a first-order reaction with time the concentration of the reactant decreases:
A.Linearly
B.Exponentially
C.No Change
D.None of these

Answer 1

In a first-order reaction, the reaction rate is directly proportional to the concentration of the reactant. If one the concentration of reactant is doubled then the reaction rate doubles or if the concentration of reactant gets increased by a factor of 10 then the reaction rate increases by a factor of 10.
$[A]\, = \,[{A_0}]{e^{ - kt}}$

Complete step-by-step answer: In such types of reactions, the concentration of only one reactant gets dependent and such kinds of reactions follow the first-order reaction. There can be multiple reactants, but only one reactant gets affected on the rate of the reaction. Whereas, the concentration of remaining reactants won’t get affected in the reaction.
Considering one example,
${N_2}{O_5}\, \to \,{N_2}{O_3}\, + {\text{ }}{O_2}$
$Rate\, = \,k\,[{N_2}{O_5}]$
The rate law for a chemical reaction is an equation which relates the reaction rate with the concentrations of a reactant or partial pressure of the reactant.
Let’s consider the general example,
$xA\, + \,yB\, \to \,C$
the rate law is given by:
$r\, = \,k\,{[A]^x}\,{[B]^y}$
In this reaction, $[A]$ and $[B]$ express the concentration of the reactants in units of moles per litres. The exponent $x$ and $y$ vary for every reaction. $k$ is the rate constant of the reaction. The value of this coefficient $k$ will vary with conditions that affect the reaction rate, such as temperature, pressure, surface area, etc. A larger rate constant indicates a faster reaction whereas the smaller rate constant indicates a slower reaction.
A first-order of the reaction is a reaction that proceeds at a rate which depends upon the linearity of only one reactant concentration among many reactants (if any multiple reactants are there it depends only upon one reactant).
For the first order reaction:
$rate\, = \, - \dfrac{{\Delta [A]}}{{\Delta t}}\, = \,k[A]$
$[A] = [{A_0}]{e^{ - kt}}$
Where,
$[A] = \,{\text{concentration}}\,{\text{of}}\,{\text{reactant}}$
$[{A_0}] = {\text{concentration}}\,{\text{of}}\,{\text{reactant at time 0 or t = 0}}$
$k\, = \,{\text{rate}}\,{\text{constant}}$
$e\, = \,{\text{base}}\,{\text{of natural logarithm}}$
By taking the natural logarithms we get;
$\ln [A]\, = \,\ln [{A_0}]\,{e^{ - kt}}$
The algebraic equation for the straight line will be;
$y\, = \,mx\, + \,c$
$y\, = \,\ln [A]$
$c\, = \,\ln [{A_0}]$
The plot of the graph is between $\ln [A]\,$ versus $t$

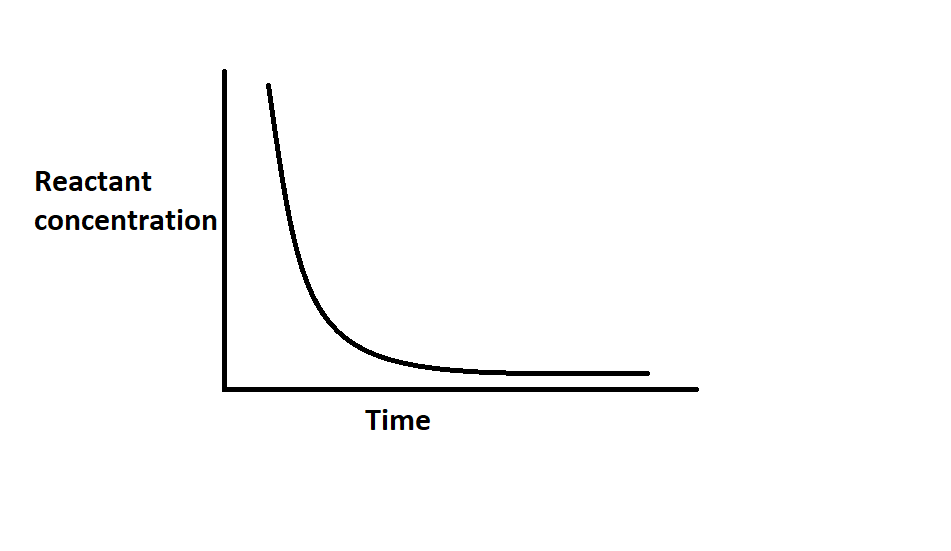
The concentration of reactants decreases with the increase inp time in an exponential manner.

So, the correct option is option (B).

Note: In a first-order reaction, the reaction depends only upon one reactant concentration. Sometimes, the first-order reaction is also referred to as a unimolecular reaction. In the first-order reaction, the concentration of the reactant decreases exponentially with the increase of time.