Question
Question: In a figure, a crescent is formed by two circles which touch at A. C is the centre of a larger circl...
In a figure, a crescent is formed by two circles which touch at A. C is the centre of a larger circle. The width of the crescent at BD is 9 cm and at EF is 5cm. Find the radii of two circles.
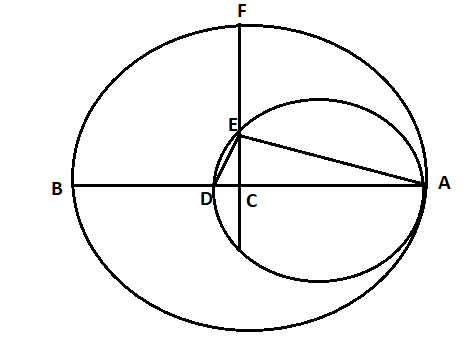
Solution
According to given in the question we have to determine the radii of two circles. When in a figure, a crescent is formed by two circles which touch at A. C is the centre of a larger circle. The width of the crescent at BD is 9 cm and at EF is 5cm. So first of all we have to let the radii of two circles. As mentioned in the question that the width of the crescent at BD is 9 cm and at EF is 5cm. So we have to determine the difference between the both of the radius we let.
Now we have to join line AE and DE and let the ∠CAE to determine the ∠AEC and now we have to consider the ΔACE and ΔDCE to determine the ∠ECD and to make both of triangles congruent to each other.
Now we have to apply the congruent rule for both of the triangles ΔACE and ΔECD. We can also understand this with the help of the diagram given below.

Formula used:
⇒(a−b)2=a2+b2−2ab……………………………………(A)
Now we have to substitute all of the values to determine both of the radiuses.
Complete step by step answer:
Step 1: First of all we have to let the radius of both circles. So let the radius of the larger circle is R and let the radius of the smaller circle is r which we can understand with the help of the diagram as below:
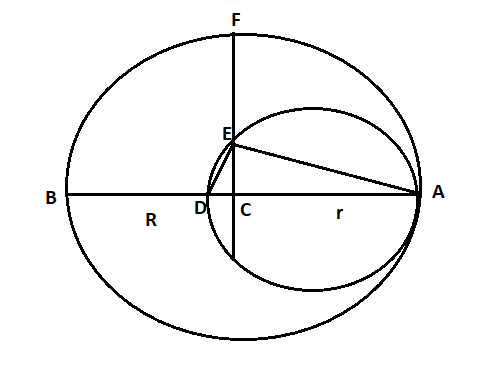
Step 2: Now as mentioned in the question the length of BD is 9cm so we can determine the difference between the diameters of the both circles.
⇒2R−2r=9 ⇒R−r=29 ⇒R−r=4.5........................(1)
Step 3: Now we have to join the line AE and DE and we have to let the ∠CAE is θ, to determine the ∠AEC we can also understand with the help of the diagram as given below,
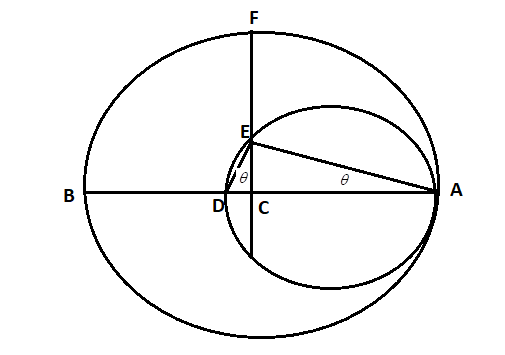
Step 4: Now we have to determine the ∠DEC with the help of ∠AED and ∠AEC
⇒∠AED=900 ⇒∠AED=∠AEC+∠DEC
On substituting all the angles in the expression obtain just above,
⇒∠DEC=900−(900−θ) ⇒∠DEC=θ
Step 5: Now, we have to make the ΔACE and ΔDCE congruent with the help of AA similarity criterion rule.
⇒∠CAE=∠CED=θ and
⇒∠ACE=∠ECD=900
Now, we can say that,
⇒ECAC=CDCE………………………………..(2)
Step 6: Now, as we know that, EC=CF−EF and CD=BC−BD. So, now substituting all the values in expression (2) as obtain in the solution step 5
⇒CF−EFAC=BC−BDCF−EF
On substituting all the values in the expression above,
⇒R−5R=R−9R−5 ⇒R(R−9)=(R−5)(R−5) ⇒R2−9R=(R−5)2
Now, to solve quadratic expression as obtained just above, we have to use the formula A as mentioned in the solution hint.
⇒R2−9R=R2+25−10R ⇒−9R=25−10R ⇒−9R+10R=25 ⇒R=25cm
Step 7: On substituting this value of R in the expression (1) as obtain in the solution step (2)
⇒25−r=4.5 ⇒25−4.5=r ⇒r=20.5cm
Hence, as mentioned in the formula (A) as mentioned in the solution hint. We have determined both of the radiuses which are R=25cm and r=20.5cm.
Note: It is necessary to make both of the triangles ΔACE and ΔECD with the help of the AA rule in which we have to make to angles similar to each other to make the triangles congruent to each other to determine the radiuses.
To find the radiuses we have to substitute the lines as EC=CF−EF and CD=BC−BD so that we can easily solve the expression obtained.
