Question

In a double star system, two stars of masses $m$ and $2m$ separated by a distance d rotate about their centre of mass. Then their common angular velocity would be
A. $\sqrt{\dfrac{Gm}{{{d}^{3}}}}$
B. $\sqrt{\dfrac{3Gm}{{{d}^{3}}}}$
C. $\sqrt{\dfrac{2Gm}{{{d}^{3}}}}$
D. $\sqrt{\dfrac{3Gm}{2{{d}^{3}}}}$

Answer 1

As a very first step, one could read the question well and hence note down the given values. Now, one could recall the equilibrium condition for the system along with the expressions for centrifugal force and the gravitational force. Also find the position of the centre of mass of the system and hence find the answer.

Formula used:
Gravitational force,
${{F}_{G}}=\dfrac{Gm\left( 2m \right)}{{{d}^{2}}}$
Centrifugal force,
${{F}_{C}}=m{{\omega }^{2}}r$

Complete step-by-step solution:
In the question, we are given a double star system in which two stars of masses $m$and $2m$are present separated by a distance of d between them and they are rotating about its centre of mass. We are supposed to find the common angular velocity of this system.

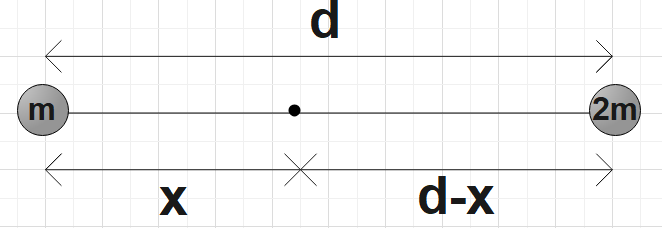
Assume that the star with mass ${{m}_{1}}$is present at origin, then the position of centre of mass could be given by,
${{r}_{CM}}=\dfrac{{{m}_{1}}{{r}_{1}}+{{m}_{2}}{{r}_{2}}}{{{m}_{1}}+{{m}_{2}}}$
$\Rightarrow {{r}_{CM}}=\dfrac{m\times 0+2m\times d}{m+2m}=\dfrac{2md}{3m}=\dfrac{2d}{3}$………………………………………………….. (1)
We know that, at equilibrium of the system, the gravitational force between the two planets would be balanced by the centrifugal force.
Gravitational force on the system would be,
${{F}_{G}}=\dfrac{Gm\left( 2m \right)}{{{d}^{2}}}$………………………………………. (2)
Now for the planet of mass m revolving around the centre of mass of the system with angular velocity $\omega$, the centrifugal force would be given by,
${{F}_{C}}=m{{\omega }^{2}}r$……………………………………………… (3)
We could equate (2) and (3) for equilibrium,
$m{{\omega }^{2}}r=\dfrac{2G{{m}^{2}}}{{{d}^{2}}}$
Putting (1),
$m{{\omega }^{2}}\left( \dfrac{2d}{3} \right)=\dfrac{2G{{m}^{2}}}{{{d}^{2}}}$
$\Rightarrow {{\omega }^{2}}=\dfrac{3Gm}{{{d}^{3}}}$
$\therefore \omega =\sqrt{\dfrac{3Gm}{{{d}^{3}}}}$
Therefore, we found the common angular velocity to be,
$\omega =\sqrt{\dfrac{3Gm}{{{d}^{3}}}}$
Option B is correct.

Note: Now we have the expression for the time period of revolution to be given by,
$T=\dfrac{2\pi }{\omega }$
On substituting the final solution into this expression, we get the time period to be,
$T=2\pi \sqrt{\dfrac{{{d}^{3}}}{3Gm}}$
Now, we have the values of these quantities to be substituted, we could easily get the time period of revolution.