Question

In a displacement method, the distance between object and screen is $96\,cm$. The ratio of lengths of two images formed by a converging lens placed between them is $4$. Then
A. Ratio of the length of object to the length of shorter image is $2$
B. Distance between the two positions of the lens is $32\,cm$
C. Focal length of the lens is $64/3\,cm$
D. When the shorter image is formed on the screen, distance of the lens from the screen is $32\,cm$

Answer 1

Here first we have to find the ratio of length of the object to the length of the shorter image. Then we have to find the distance and then we have to find the focal length $f$ . At last we have to find the shorter image on the screen.

Complete step by step answer:
Given,
Ratio of lengths of two images formed by a converging lens placed between them is $4$
, $\dfrac{{{I_1}}} {{{I_2}}} = 4$ ...... (1)
The distance between object and screen is $96\,cm$

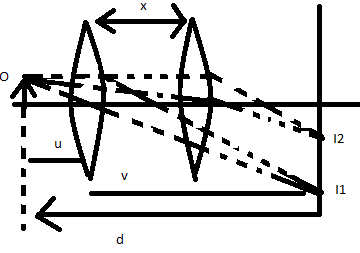
From the figure we can see that image ${I_2}$ is smaller than image ${I_1}$
Also $D$ is the distance between the image and object. And $x$ is the distance between the lenses.
So focal length, $f$ will be $f = \dfrac{{{D^2} - {x^2}}} {{4D}} = \dfrac{x} {{{m_1} - {m_2}}}$ , where ${m_1}$ is the magnification of lens $1$ and ${m_2}$ is the magnification of lens $2$.
First let us see option A-
So, ${m_1} = \dfrac{{{I_1}}} {O},\,{m_2} = \dfrac{{{I_2}}} {O}$
${m_1}{m_2} = 1$
$O = \sqrt {{I_1}{I_2}}$
$\dfrac{O} {{{I_1}}} = ?$
$O = \sqrt {{I_1} \times \dfrac{{{I_1}}} {4}} \\\ O = \dfrac{{{I_1}}} {2} \\\ {O} {{{I_1}}} = \dfrac{1} {2} \\\$
${O} {{{I_2}}} = ?$
Therefore, using equation (1) we get-
$O = \sqrt {4{I_1}{I_2}} \\\ \dfrac{O} {{{I_2}}} = 2 \\\$
${m_1} = 2,\,{m_2} = \dfrac{1} {2}$
Hence, option A is correct. Ratio of the length of object to the length of shorter image is $2$
Now let us see option B-
From the figure and given part we get-
For first image
$u + v = 96\,cm$ ...... (2)
Also
$\dfrac{v} {u} = 2 \\\ v = 2u$ ...... (3)
From equation (2) and (3), we get-
$3u = 96 \\\ u = 32\,cm \\\ v = 64\,cm \\\$
For second image, we get-
$\dfrac{v}{u}\,=\,\dfrac{1}{2}$
u = 2v
3v = 96 cm
v = 32 cm
Therefore, $x = 64 - 32 = 32\,cm$ (for both the cases)
Hence, option B is also correct. Distance between the two positions of the lens is $32\,cm$
Now let us see option C-
Here we use the formula for the focal length,
f = \dfrac{x} {{{m_1} - {m_2}}} \\\ = \dfrac{{32}}{{2 - \dfrac{1} {2}}} \\\ = \dfrac{{64}} {3} \\\
Hence, option C is also correct. Focal length of the lens is $64/3\,cm$
For option D- Option D is also correct since from the second case in option B we can see that- When the shorter image is formed on the screen, distance of the lens from the screen is $32\,cm$

So, the correct answer is “Option B”.

Note:
Here we have to calculate $v$ and $u$ for both the images otherwise we shall not get the desired answer.
Also we have to carefully establish the formulae for all the cases.