Question
Question: In a \(\Delta PQR\) Let \(\angle PQR={{30}^{\circ }}\) and the sides PQ and QR have length \(10\sqrt...
In a ΔPQR Let ∠PQR=30∘ and the sides PQ and QR have length 103 and 10 respectively, then which of the following statement is/are true? This question has multiple options correct.
& \text{A}.\angle QPR={{45}^{\circ }} \\\ & \text{B}.\text{ The area of triangle PQR is 25}\sqrt{3}\text{ and }\angle \text{QRP=12}{{\text{0}}^{\circ }} \\\ & \text{C}.\text{ The radius of the in circle of the triangle PQR is 10}\sqrt{3}-15 \\\ & \text{D}.\text{ The area of circumcircle of the triangle PQR is 100}\pi \\\ \end{aligned}$$Solution
To solve this question, we will first calculate length of side PR using formula cosθ=2bcb2+c2−a2 where ABC is a triangle as given below:
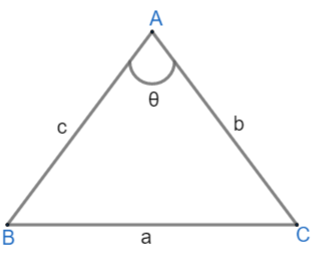
Side length AB = c, BC = a and AC = b. Also, ∠BAC=θ
After this, we will calculate area of triangle formed by using formula:
Area=21×cbsinθ
Where ABC triangle is as above.
After this we will solve option C and option D by using the formula of radius of incircle and radius of circumcircle of triangle, it is given as radius of incircle of Δ=Sarea of Δ where S=2a+b+c in ΔABC above and radius of circumcircle=sin2θa where ∠BAC=θ and a=BC in above ΔABC
Complete step by step answer:
Consider the triangle given as PQR below:
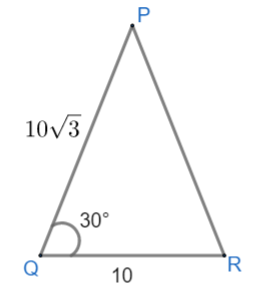
Given ∠PQR=30∘, QR = 10 and PQ=103
First of all we will calculate the value of length PR for that we will use cosθ which is given by:
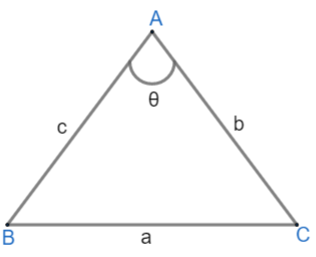
If ΔABC is there and angle ∠A=θ then cosθ=2bcb2+c2−a2
We will use this formula to calculate length PR of ΔPQR
We have PQ=103 let it be b of above equation.
QR = 10 let it be c of above equation and θ=30∘
Then, using formula we have,
