Solveeit Logo
Login

Question

Question: In a cyclic quadrilateral ABCD, if \(AB||CD\) and \(\angle B={{70}^{\circ }}\) . Find the remaining ...

In a cyclic quadrilateral ABCD, if AB∣∣CDAB||CD and ∠B=70∘\angle B={{70}^{\circ }} . Find the remaining angle.

Explanation

Solution

Hint: Property of cyclic quadrilaterals can be given as “sum of opposite angles in cyclic quadrilateral will always be180∘{{180}^{\circ }}“. And can be given as “sum of angles formed by a transversal on the same side of two parallel lines is 180∘{{180}^{\circ }}“.

“Complete step-by-step answer:”
Here, we have a cyclic quadrilateral ABCD, with AB∣∣CDAB||CD and ∠B\angle B and hence, we need to determine the remaining angles of quadrilateral ABCD i.e. ∠C,∠A,∠D\angle C,\angle A,\angle D. First of all, let us draw a neat diagram with the help of given information:

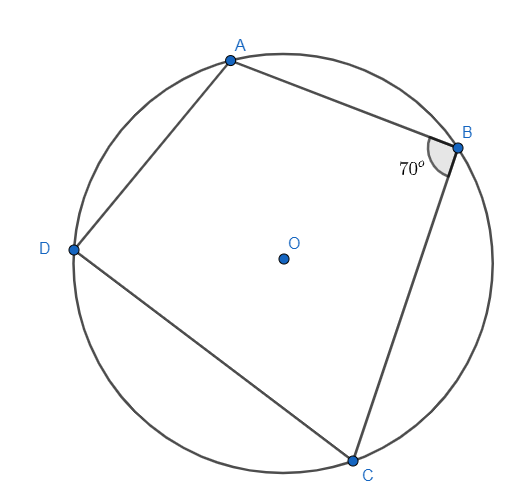
As we know cyclic quadrilateral lies in a circle and all vertices of it will touch the circumference of the circle. So, here ABCD is lying inside a circle with ∠B=70∘\angle B={{70}^{\circ }} , O as a centre and AB∣∣CDAB||CD .
Here, we need to use two properties to solve this problem, first property of cyclic quadrilateral and second of parallel lines.
The property of a cyclic quadrilateral is, the sum of opposite angles of any cyclic quadrilateral is 180∘{{180}^{\circ }} . Hence, from the given diagram we get,
∠B+∠D=180∘............(i) ∠A+∠C=180∘............(ii) \begin{aligned} & \angle B+\angle D={{180}^{\circ }}............\left( i \right) \\\ & \angle A+\angle C={{180}^{\circ }}............\left( ii \right) \\\ \end{aligned}
Now, another property of parallel lines can be given as that sum of angles on the side of a transversal to two parallel lines is 180∘{{180}^{\circ }} . Transversal is a line which cuts two parallel lines.

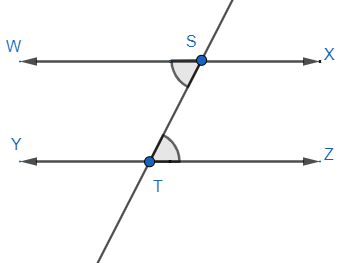
So, from the above property we have,
∠WST+∠STY=180∘\angle WST+\angle STY={{180}^{\circ }} and ∠XST+∠STZ=180∘\angle XST+\angle STZ={{180}^{\circ }}
Hence, AD and BC are acting as a transversal for parallel lines AB and CD.
So, we can get equation from the cyclic quadrilateral ABCD as
∠A+∠D=180∘............(iii) ∠B+∠C=180∘............(iv) \begin{aligned} & \angle A+\angle D={{180}^{\circ }}............\left( iii \right) \\\ & \angle B+\angle C={{180}^{\circ }}............\left( iv \right) \\\ \end{aligned}
As we know the value of ∠B\angle B is given in the problem as ∠B=70∘\angle B={{70}^{\circ }} . Hence, put it in equation (i) to get ∠D\angle D , so we get,
70∘+∠D=180∘ ∠D=180∘−70∘ ∠D=110∘ \begin{aligned} & {{70}^{\circ }}+\angle D={{180}^{\circ }} \\\ & \angle D={{180}^{\circ }}-{{70}^{\circ }} \\\ & \angle D={{110}^{\circ }} \\\ \end{aligned}
Now, put ∠B=70\angle B=70 in equation (iv) to get the value of ∠C\angle C . So, we get
70∘+∠C=180∘ ∠C=180∘−70∘ ∠C=110∘ \begin{aligned} & {{70}^{\circ }}+\angle C={{180}^{\circ }} \\\ & \angle C={{180}^{\circ }}-{{70}^{\circ }} \\\ & \angle C={{110}^{\circ }} \\\ \end{aligned}
Now, ∠A\angle A is remaining, so let us put value of ∠C=110∘\angle C={{110}^{\circ }} in the equation (ii) to get ∠A\angle A .8 Hence, we get
∠A+110∘=180∘ ∠A=180∘−110∘ ∠A=70∘ \begin{aligned} & \angle A+{{110}^{\circ }}={{180}^{\circ }} \\\ & \angle A={{180}^{\circ }}-{{110}^{\circ }} \\\ & \angle A={{70}^{\circ }} \\\ \end{aligned}
Hence, all the angles of cyclic quadrilateral can be given as ∠A=70∘,∠B=70∘,∠C=110∘,∠D=110∘\angle A={{70}^{\circ }},\angle B={{70}^{\circ }},\angle C={{110}^{\circ }},\angle D={{110}^{\circ }}

Note: One may try to apply only one property he or she may know only one property i.e. property of cyclic quadrilateral or property of parallel lines. One cannot get answers by using only one property of them. So, be clean with the both properties mentioned in the solution.
One may try to apply the property of a simple quadrilateral as that sum of all interior angles is 360∘{{360}^{\circ }} of it. It will not work here to get values of all the angles.