Solveeit Logo
Login

Question

Question: In a cubic structure of diamond which is made from \(X\) and \(Y\) , where \(X\) atoms are at the co...

In a cubic structure of diamond which is made from XX and YY , where XX atoms are at the corners of the cube and YY at the face centres of the cube . The molecular formula of the compound is :
A: X2Y{X_2}Y
B: X3Y{X_3}Y
C: XY2X{Y_2}
D: XY3X{Y_3}

Explanation

Solution

Whenever we are given a solid cube of a molecule , the positions of the substituent atoms determine the molecular formula of the compound. If the atom is in the edge centre it contributes $$$$$\dfrac{1}{4}totheparticularmolecule,ifitisinthefacecentreitcontributesto the particular molecule , if it is in the face centre it contributes\dfrac{1}{2}tothemoleculeandifitisinthecornerofthecubeitcontributesto the molecule and if it is in the corner of the cube it contributes\dfrac{1}{8}$ to the molecule.

Complete step by step answer:

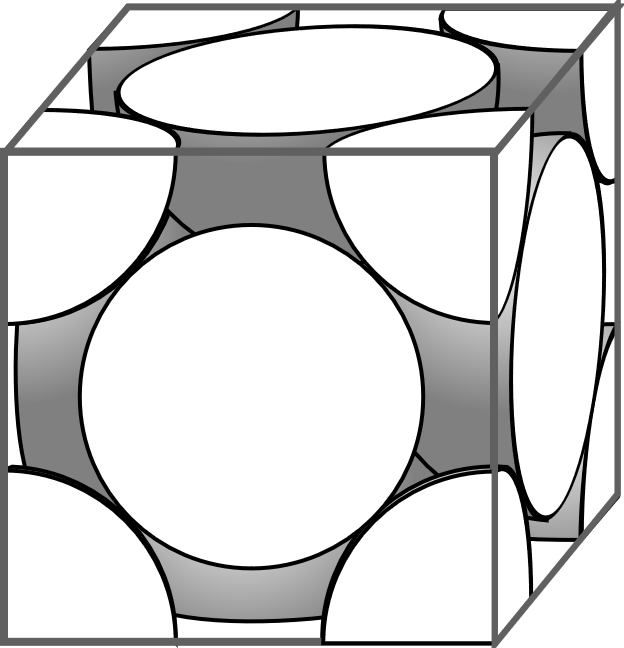
                                                       ![](https://www.vedantu.com/question-sets/6e7964b4-322b-45ca-9cdd-15120ab050291825031822581005186.png)

In the given question it is given that the XX atoms are in the corners and the YY atoms are in the face centre. In a given cube there are eight corners and six faces. So there will be eight XX atoms in the eight corners of the cube and six YY atoms in the six faces of the cube. The contribution of the corner atoms to a cube is 18\dfrac{1}{8} to the compound and the contribution of the face centred atoms to the compound is 12\dfrac{1}{2} . So the molecular formula of the compound will be
X18×8Y12×6=XY3{X_{\dfrac{1}{8}}}_{ \times 8}{Y_{\dfrac{1}{2}}}_{ \times 6} = X{Y_3}
**So from a the above explanation and calculation it is clear that the correct answer of the question is
D: XY3X{Y_3} **

Additional information : When a cube has eight atoms in eight corners and one atom in the body centre it is known as body centred cube. When a cube has eight atoms in eight corners and six atoms in the six faces of the cube it is known as a face centred cube.

Note: Always remember that the atoms in the corner constitute 18\dfrac{1}{8} the compound , atoms in faces contributes 12\dfrac{1}{2} ,atoms in the edge centre contributes 14\dfrac{1}{4} and atoms in body centre contributes 1 to the compound. To find the molecular formula of the compound multiply the number of atoms in the particular positions with their respective contribution to the compound.