Question

In a concave mirror experiment, an object is placed at a distance ${x}_{1}$from the focus and the image is formed at a distance${x}_{2}$ from the focus. The focal length of the mirror would be
A.${x}_{1}{x}_{2}$
B.$\sqrt {{x}_{1}{x}_{2}}$
C.$\dfrac {{x}_{1}+{x}_{2}}{2}$
D.$\sqrt {\dfrac{{x}_{1}}{{x}_{2}}}$

Answer 1

Using the mirror formula this numerical can be solved. To solve this problem, you should know the difference between the mirror formula for concave mirror and convex mirror. Substitute the values for object distance and image distance. And thus, find the value for focal length of the concave mirror.
Formula used:
$\dfrac {1}{v}+ \dfrac {1}{u}= \dfrac {1}{f}$

Complete answer:

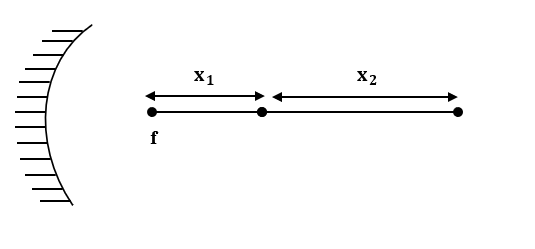
Given: Object distance= $({x}_{1}+f)$
Image distance = $({x}_{2}+f)$
Focal length = f
Using mirror formula,
Where, v is the distance of the image from the mirror
u is the distance of the object from the mirror
f is the focal length of the mirror
$\dfrac {1}{v}+ \dfrac {1}{u}= \dfrac {1}{f}$
Substituting values in above equation we get,
$\dfrac {1}{({x}_{2}+f)}+ \dfrac {1}{({x}_{1}+f)}= \dfrac {1}{f}$
$\Rightarrow \dfrac {1}{f}= \dfrac {({x}_{1}+f)+ ({x}_{2}+f)} {({x}_{1}+f)({x}_{2}+f)}$
$\Rightarrow f= \sqrt {{x}_{1}{x}_{2}}$
Thus, the focal length of the mirror would be $\sqrt{{x}_{1}{x}_{2}}$.

Hence, the correct answer is option B i.e. $\sqrt {{x}_{1}{x}_{2}}$

Note:
For solving such types of questions you should know the sign conventions. For a concave mirror, if the image and object are on the same side and in front of the mirror then the image distance is positive. But if the image is formed behind the mirror that is on the opposite side of the mirror and object then the image distance is negative. Focal length of the concave mirror is positive and focal length of the convex mirror is negative.