Question

In a concave mirror, an object is placed at a distance $d_{1}$ from the focus and the image is formed at a distance $d_{2}$ from the focus. Then the focal length of the mirror is:

& A.\sqrt{{{d}_{1}}{{d}_{2}}} \\\ & B.{{d}_{1}}{{d}_{2}} \\\ & C.\frac{{{d}_{1}}+{{d}_{2}}}{2} \\\ & D.\sqrt{\frac{{{d}_{1}}}{{{d}_{2}}}} \\\ \end{aligned}$$

Answer 1

The mirror formula is the relationship between the distance of an object $u$ , distance of image $v$ and the focal length of the lens $f$. This law can be used for both concave and convex mirrors with appropriate sign conventions. This sum is similar to an object placed in front of a spherical mirror. Hence using spherical mirror formula, we can find the image distance.
Formula:
$\dfrac{1}{u}+\dfrac{1}{v}=\dfrac{1}{f}$

Complete answer:
We know that a mirror reflects or bounces back, only a fraction of the beam of light in a single direction, as compared to other objects which either scatter light or absorb it. They are used to see one's reflection, like the normal mirror we use in house, or are used to see objects that are not visible directly, like rear mirrors and dentist’s mirror. There are various types of mirrors on the basis of shapes, like plane mirrors , the ones we use generally, which provide real images and curved mirrors, which may distort or magnify the image, generally seen in mirror mazes.
Let us assume that the focal length of the concave mirror is $f$. Let the object distance be $u$ and the image distance be $v$ from the mirror. Consider the image shown below, we have $MO=u$, $MI=v$ and $MF=f$. Given that, $OF={{d}_{1}}$ and $IF={{d}_{2}}$.
Then we have, $u=f+d_{1}$ and $v=f+d_{2}$

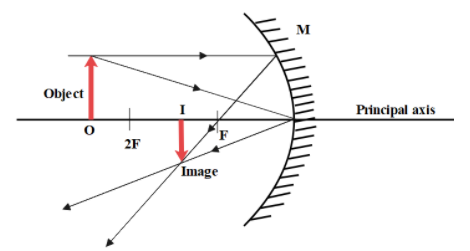
Then, substituting the values in the mirror formula, we get, $\dfrac{1}{f}=\dfrac{(f+d_{1})+(f+d_{2})}{(f+d_{1})(f+d_{2})}$
$\implies (f+d_{1})(f+d_{2})=f(f+d_{1}+f+d_{2})$
$\implies f^{2}+fd_{1}+fd_{2}+d_{1}d_{2}=2f^{2}+fd_{1}+fd_{2}$
$\implies 2 f^{2}-f^{2}=d_{1}d_{2}$
$\implies f=\sqrt{d_{1}d_{2}}$

Thus the correct answer is option (A) $\sqrt{{{d}_{1}}{{d}_{2}}}$.

Note:
Mirror reflects or bounces back, only a fraction of the beam of light in a single direction. Be careful with the sign conventions used. Also note that the focal length is half the radius of curvature of the spherical mirror.