Question

In a compound microscope the lens used are
A. Both convex of same focal length
B. both convex of different focal length
C. both concave of same focal length
D. one convex and one concave of different focal length.

Answer 1

A compound microscope is an optical device which produces magnified images of tiny objects. A good quality compound microscope can produce magnification in order of $1000$. In compound two lenses were used so that the combined magnification of the compound microscope is increased and a much magnified image of the tiny object is seen in the eye piece. The length of two lenses used is different. The objective (the lens near the object) is of small size whereas the eyepiece (the lens near the eye) is of different size.

Formulas used:
Magnification of compound microscope is given by.
$M=\dfrac{{{\theta }_{1}}}{{{\theta }_{0}}}$
Where ${{\theta }_{1}}\text{ and }{{\theta }_{0}}$are the angle subtended by image and object at the eyepiece.
Magnification of simple microscope of focal length $f$ and distance of image from the lens $D$ is
$M=1+\dfrac{D}{f}$

Complete answer:
The convex lens ‘O’ of short focal length and small aperture, which faces the object to be viewed, is known as the objective. The convex lens ‘E’ of large focal length and comparatively large aperture, near the eye, is known as eyepiece. The two lenses are placed in two metal tubes so as to have a common principal axis. The eyepiece is fitted in a draw-tube and can be slided within the main tube by means of rack and pinion arrangement to focus the microscope upon the object.
Let AB be an extended object situated on the principal axis at a distance slightly greater than the focal length of the objective. As refraction takes place through the objective ‘0’, a real, inverted and magnified image ${{A}_{1}}{{B}_{1}}$ is formed. The lens E is so adjusted that ${{A}_{1}}{{B}_{1}}$ falls within its focal length and so the final virtual image ${{A}_{2}}{{B}_{2}}$of ${{A}_{1}}{{B}_{1}}$ is obtained at the least distance of distinct vision 'D' from the eye. The final image ${{A}_{2}}{{B}_{2}}$ is thus highly magnified but is inverted with respect to the object $AB$.

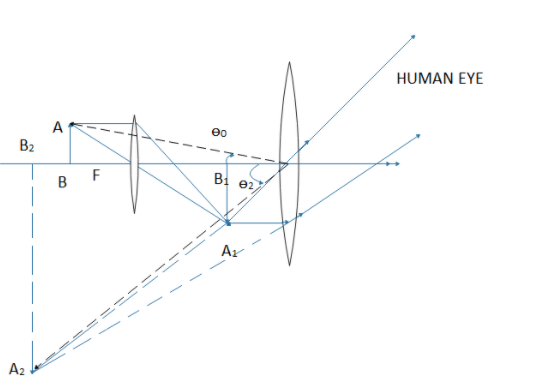
When the final image is obtained at the least distance of distinct vision from the eye.
The magnifying power of a compound microscope is defined as the angle subtended by the final image at the eye to the angle subtended by the object at the eye when both the object and the image are situated at the distance of distinct vision from the eye.
If the object is situated at ${{B}_{2}}$, it would have occupied the length such that ${{B}_{2}}C=AB$.
Let the angles subtended by the object ${{B}_{2}}C$and final image ${{A}_{2}}{{B}_{2}}$at the eye be ${{\theta }_{0}}\text{ and }{{\theta }_{1}}$ respectively
Then the magnification of the compound microscope will be
$M=\dfrac{{{\theta }_{1}}}{{{\theta }_{0}}}=\dfrac{\tan {{\theta }_{1}}}{\tan {{\theta }_{0}}}\left( \because \text{ because }{{\theta }_{1}}\text{and}{{\theta }_{0}}\text{ are very small} \right)$
In triangle ${{O}_{2}}{{B}_{2}}C,$ $\tan {{\theta }_{0}}=\dfrac{{{B}_{2}}C}{{{O}_{2}}{{B}_{2}}}=\dfrac{AB}{{{O}_{2}}{{B}_{2}}}$
In triangle ${{O}_{2}}{{B}_{2}}{{A}_{2}},$ $\tan {{\theta }_{1}}=\dfrac{{{A}_{2}}{{B}_{2}}}{{{O}_{2}}{{B}_{2}}}$
Now magnification
$M=\dfrac{\tan {{\theta }_{1}}}{\tan {{\theta }_{0}}}=\left( \dfrac{\dfrac{{{A}_{2}}{{B}_{2}}}{{{O}_{2}}{{B}_{2}}}}{\dfrac{AB}{{{O}_{2}}{{B}_{2}}}} \right)=\dfrac{{{A}_{2}}{{B}_{2}}}{AB}=\dfrac{{{A}_{2}}{{B}_{2}}}{{{A}_{1}}{{B}_{1}}}\times \dfrac{{{A}_{1}}{{B}_{1}}}{AB}$
But the magnification of objective is ${{M}_{1}}=\dfrac{{{A}_{1}}{{B}_{1}}}{AB}$ and that of eyepiece is ${{M}_{2}}=\dfrac{{{A}_{2}}{{B}_{2}}}{{{A}_{1}}{{B}_{1}}}$
So, $M={{M}_{1}}\times {{M}_{2}}$
For objective lens
$\begin{aligned} & \text{Magnification}=\dfrac{\text{distance of image}}{\text{distance of object}}=\dfrac{v}{u} \\\ & \Rightarrow {{M}_{1}}=\dfrac{v}{u} \\\ \end{aligned}$
Also the eyepiece acts like a simple microscope so its magnification is given by ${{M}_{2}}=1+\dfrac{D}{{{f}_{e}}}$
Where ${{f}_{e}}=\text{ focal length of eyepiece}$
Now the magnification of compound microscope is given by
$M=\dfrac{v}{u}\left( 1+\dfrac{D}{{{f}_{e}}} \right)$
If the object $AB$ is situated very near the principal focus of the objective, the image ${{A}_{1}}{{B}_{1}}$will be far removed from the lens ‘O’. In that case
$u=f=\text{focal length of the objective}$
$v=L=\text{length of the microscope tube}$.
So magnification of compound microscopes now becomes.
$M=\dfrac{L}{{{f}_{0}}}\left( 1+\dfrac{D}{{{f}_{e}}} \right)$
So in order to have large magnification the objective lens and eyepiece lens should have small focal length.
In a compound microscope the length of objective is less than the length of eyepiece. So the focal length of the lens should be smaller than the eyepiece.

So the correct option is. B.

Note:
The resolving power of a compound microscope is the inverse of the distance between the two points that can be resolved. For a high resolving power the refractive index must be more. For a good microscope the magnification must be large. In a compound microscope the combination of lenses are used to get a good quality image.