Question
Question: In a community of 175 persons, 40 read the Times, 50 reads the Samachar and 100 do not read any. How...
In a community of 175 persons, 40 read the Times, 50 reads the Samachar and 100 do not read any. How many people read both the papers?
(a) 10
(b) 15
(c) 20
(d) 25
Solution
Hint: First, we have to draw a Venn diagram representing all the value given to us in question. Then finding people who read both or any single newspaper which will be considered as n(T∪S) . After this we will use the formula of union i.e. n(T∪S)=n(T)+n(S)−n(T∩S) . Thus, we will get the answer of the intersection part.
Complete step-by-step answer:
Here, we have total number of people i.e. Universal set denoted as U is 175 persons. In Mathematical form written as, n(U)=175
Now, the number of people reading Times is denoted as n(T)=40 and number of people reading Samachar is denoted as n(S)=50 . People who are not reading any newspaper are 100. We have to find people who read both the newspaper i.e. Times and Samachar. So, this can be shown using the Venn Diagram as below.
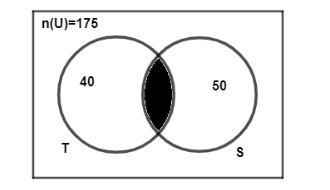
As shown in the above diagram, T is for Times, S is for Samachar and centre which is black we have to find value for that which is people who read both times and Samachar.
Now, to find people who read newspaper either both or any single is equal to total people minus people who do not read any newspaper, written as
People who read newspaper both or any one =n(U)−100
=175−100=75
So, people who read newspapers are a total of 75 people.
Now, we want to find people who read both the paper means we have to find intersection of times and Samachar using the set theory formula given as,
n(T∪S)=n(T)+n(S)−n(T∩S)
So, we have values n(T∪S)=75,n(T)=40,n(S)=50 substituting this, we get
⇒75=40+50−n(T∩S)
Which on solving, we get
⇒n(T∩S)=90−75=15
So, people who read both the papers are 15.
Hence, option (b) is correct.
Note: Another approach to solve the above sum is by taking the intersection part as x. Also, people from Times and Samachar will be reading both the paper so, subtracting x from value 40 and 50 also. As per the Venn diagram, it is shown as below:
So, we will find first people who reads newspaper is =n(U)−100
=175−100=75 . So, we will now simply add the values of the set and equate it with 75. We get,
⇒40−x+x+50−x=75
On solving, we get
⇒90−x=75
⇒x=15 Thus, from this also we get the same answer.
