Question

In a colony, $275$ families buy Tamil newspapers, $150$ families buy English newspaper, $45$ families buy Hindi newspaper, $125$ families buy Tamil and English newspapers, $17$ families buy English and Hindi newspaper, $5$ families buy Tamil and Hindi newspaper, and $3$ families buy all the three newspapers, then find the number of families buy only one newspapers.

Answer 1

Here the given problem is some information that in a colony of families which number of people buy which language newspapers. We have to find the number of families for the required result. Substituting the given values into the probability relation we will get the required result. Then, using the formula and given information we can find the number of families who buy only one newspaper.

Formula used: We will apply the formula of $n(D) = n(A) + n(B) + n(C) - 2[n(A \cup B) + n(B \cup C) + n(C \cup A)] - 3n(A \cap B \cap C)$
Here $A$, $B$, $C$ be the number of families who speak Tamil, English and Hindi.

Complete step-by-step answer:
It is given that;
Number of families who buy Tamil newspapers $A$ is $275$.
Number of families who buy English newspapers $B$ is $150$.
Number of families who buy Hindi newspapers $C$ is $45$.
Number of families who buy Tamil and English newspapers is $125$.
Number of families who buy Hindi and English newspapers is $17$.
Number of families who buy Tamil and Hindi newspapers is $5$.
Number of families who buy all three newspapers is $3$.
We have to find the number of families who buy only one newspaper.
So, as per the given information
$n(A) = 275$
$n(B) = 150$
$n(C) = 45$
$n(A \cap B) = 125$
$n(B \cap C) = 17$
$n(C \cap A) = 5$
$n(A \cap B \cap C) = 3$
Number of families who buy both Tamil and English newspapers is $= n(A \cup B) = 125 - 3 = 122$.
Number of families who buy both Hindi and English newspapers is $= n(B \cup C) = 17 - 3 = 14$.
Number of families who buy both Tamil and Hindi newspapers is $= n(C \cup A) = 5 - 3 = 2$.
Let us consider, the number of families who buy only one newspaper is $D$.
So,
$n(D) = n(A) + n(B) + n(C) - 2[n(A \cup B) + n(B \cup C) + n(C \cup A)] - 3n(A \cap B \cap C)$
Substitute the values we get,
\Rightarrow$$$n(D) = 275 + 150 + 45 - 2[122 + 14 + 2] - 3 \times 3$$ Solving we get, \Rightarrow$$$n(D) = 185$$

$\therefore$ The number of families buy only one newspaper is $185$

Note: We can solve the sum by using a Venn diagram.

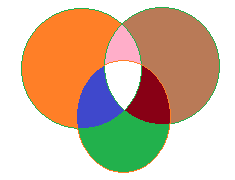
Venn diagrams use overlapping circles or other shapes to illustrate the logical relationships between two or more sets of items. Often, they serve to graphically organize things, highlighting how the items are similar and different.
Here, orange shaded part is $n(A) = 275$
Brown shaded part is $n(B) = 150$
Green shaded part is $n(C) = 45$
Pink shaded part is $n(A \cap B) = 125$
Maroon shaded part is $n(B \cap C) = 17$
Blue shaded part is $n(C \cap A) = 5$
White part is $n(A \cap B \cap C) = 3$
So, the number of families buy only one newspaper is $n(D) = 275 + 150 + 45 - 2[122 + 14 + 2] - 3 \times 3 = 185$
Hence, the number of families who buy only one newspaper is $185$.