Question

In a collinear collision, a particle with an initial speed ${{v}_{0}}$ strikes a stationary particle of the same mass. If the final total kinetic energy is 50% greater than the original kinetic energy, the magnitude of the relative velocity between the two particles, after collision, is :

& \text{A}\text{. }\dfrac{{{v}_{\circ }}}{2} \\\ & \text{B}\text{. }\dfrac{{{v}_{\circ }}}{\sqrt{2}} \\\ & \text{C}\text{. }\dfrac{{{v}_{\circ }}}{4} \\\ & \text{D}\text{. }\sqrt{2}{{v}_{\circ }} \\\ \end{aligned}$$

Answer 1

First look at the question and take out all the required values needed from it. Then draw the required diagram after and before the collision. Then apply the law of conservation of energy and label the equation got as the first question. Then apply the formula for conservation of linear momentum to find another equation label it equation 2 and then match the equation with equation one and we will get another equation label it as equation 3 then apply the formula for magnitude of relative velocity and replace all the derived values from it to get the final answer.

Formula Used:
Initial kinetic energy + Initial potential energy = final kinetic energy + Final potential
$mv={{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}}$
${{v}_{1}}^{2}-{{v}_{2}}^{2}$

Complete step by step answer:
Let us consider the initial velocity ${{v}_{0}}$as v.
Let us first look at the values that are given,
We see that there is a collinear collision, and a particle has an initial speed ${{v}_{0}}$, and this particle has the same mass as the first particle.
Now after the collision the final kinetic energy has turned 50% higher than the original kinetic energy.
So, we have to find the magnitude of relative velocity between the two particles before the collision.

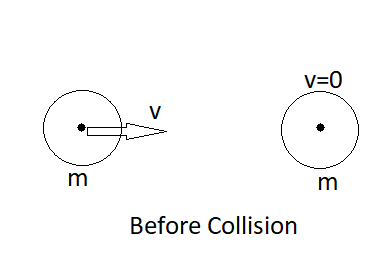
So, according to the question, here we can see that there are two particles one of the particles is moving with a velocity v and another has no velocity or is stationary, we can further see that the mass of both the bodies are the same.

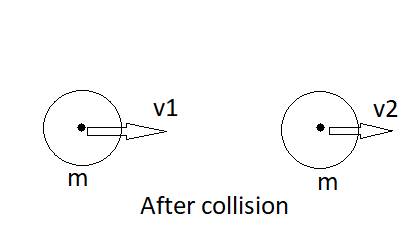
So, now after the collision the particle has also gained some velocity and started moving with velocity ${{v}_{2}}$ and the first particle lost some velocity and started moving with a velocity of ${{v}_{1}}$.
Now, we can apply the law of conservation of kinetic energy as we can see that energy is increased after the collision,
Initial kinetic energy + Initial potential energy = final kinetic energy + Final potential energy.
So,
$\Rightarrow \dfrac{1}{2}m{{v}^{2}}+\dfrac{1}{2}\left( \dfrac{1}{2}m{{v}^{2}} \right)=\dfrac{1}{2}m{{v}_{1}}^{2}+\dfrac{1}{2}m{{v}_{2}}^{2}$,
Now, on solving the above equation we get,
$\Rightarrow {{v}_{1}}^{2}+{{v}_{2}}^{2}=\dfrac{3}{2}{{v}^{2}}$ ……. Eq.1
Now, according to conservation of linear momentum,
$mv={{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}}$
Which on solving we get,
$v={{v}_{1}}+{{v}_{2}}$…… Eq.2 (as mass of both the particles are same and it never changes)
Now, as in Eq.1 we have ${{v}_{1}}^{2}+{{v}_{2}}^{2}$so we will square the Eq.2 also as we have to find a relationship between both so,
Taking eq.2 $v={{v}_{1}}+{{v}_{2}}$
Squaring both sides,
${{v}^{2}}={{\left( {{v}_{1}}+{{v}_{2}} \right)}^{2}}$,
$\Rightarrow {{v}^{2}}={{v}_{1}}^{2}+{{v}_{2}}^{2}+2{{v}_{1}}{{v}_{2}}$,
$\Rightarrow {{v}^{2}}=\dfrac{3}{2}{{v}^{2}}+2{{v}_{1}}{{v}_{2}}$, (as $\Rightarrow {{v}_{1}}^{2}+{{v}_{2}}^{2}=\dfrac{3}{2}{{v}^{2}}$)
On solving the above equation we get,
$\dfrac{{{v}^{2}}}{2}=-2{{v}_{1}}{{v}_{2}}$………. Eq.3
So, now for relative velocity,
${{\left( {{v}_{1}}^{2}-{{v}_{2}}^{2} \right)}^{2}}={{v}_{1}}^{2}+{{v}_{2}}-2{{v}_{1}}{{v}_{2}}$
$\Rightarrow {{\left( {{v}_{1}}^{2}-{{v}_{2}}^{2} \right)}^{2}}=\dfrac{3}{2}{{v}^{2}}+\dfrac{{{v}^{2}}}{2}$,
$\Rightarrow {{\left( {{v}_{1}}^{2}-{{v}_{2}}^{2} \right)}^{2}}=\dfrac{3}{2}{{v}^{2}}+\dfrac{{{v}^{2}}}{2}$,
$\Rightarrow {{\left( {{v}_{1}}^{2}-{{v}_{2}}^{2} \right)}^{2}}=2{{v}^{2}}$
$\Rightarrow {{v}_{1}}^{2}-{{v}_{2}}^{2}=\sqrt{2{{v}^{2}}}$
$\Rightarrow {{v}_{1}}^{2}-{{v}_{2}}^{2}=\sqrt{2}v$ or $\Rightarrow {{v}_{1}}^{2}-{{v}_{2}}^{2}=\sqrt{2}{{v}_{0}}$(as ${{v}_{0}}=v$.)
So, option D is the correct option.

Note:
Here in the equation $\Rightarrow \dfrac{1}{2}m{{v}^{2}}+\dfrac{1}{2}\left( \dfrac{1}{2}m{{v}^{2}} \right)=\dfrac{1}{2}m{{v}_{1}}^{2}+\dfrac{1}{2}m{{v}_{2}}^{2}$, $\dfrac{1}{2}\left( \dfrac{1}{2}m{{v}^{2}} \right)$ is done as after the collision 50% of energy will increase so there must be some place from where this 50% KE is drawn from and usually it is the potential energy that’s get converted so that is only shown here.