Question

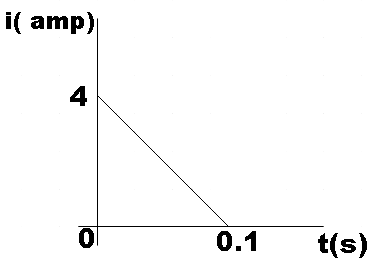
In a coil of resistance $10\Omega$ the induced current developed by changing magnetic flux through it, is shown in the figure as a function of time. The magnitude of change in flux through the coil in weber is:

A. 2
B. 6
C. 4
D.8

Answer 1

You may recall that the area under the given current-time graph will give us the value of charge flowing through the conductor. Now you may recall the expression for change in magnetic flux through the coil in terms of charge flowing through it and the resistance of the coil. Substituting these values, you will get the answer.

Formula used:
Charge flowing through the coil,
$q=\dfrac{\Delta \phi }{R}$
Current,
$i=\dfrac{dq}{dt}$

Complete answer:
In the question, we are given the variation of the induced current developed by the changing magnetic flux through a coil of resistance $10\Omega$. We are asked to find the magnitude of change in flux through the coil in weber by using the given information.
The charge passing through the given coil could be given by the expression,
$q=\dfrac{\Delta \phi }{R}$ ……………………………………………….. (1)
Where, $\Delta \phi$ is the change in magnetic flux in weber and R is the resistance of the coil.
We know that, the current passing through the coil will be the time rate of change of charge flowing in the coil. That is,
$i=\dfrac{dq}{dt}$
$\Rightarrow dq=idt$
Integrating on both sides we get,
$\int{dq}=\int{idt}$
$\Rightarrow q=\int{idt}$ ……………………………………………. (2)
But we know that value of the integral on the right hand side can be given by the area under the given graph which is a triangle. So,
$\int{idt=\dfrac{1}{2}}\times b\times h$
$\Rightarrow \int{idt}=\dfrac{1}{2}\times 0.1\times 4$
$\Rightarrow \int{idt=0.2}$
But from (2) we have,
$q=0.2C$
But from (1) we have,
$q=\dfrac{\Delta \phi }{R}$
Substituting the values of q and R, we get,
$\Delta \phi =0.2\times 10Wb$
$\therefore \Delta \phi =2Wb$
Therefore, we found the change in flux in the given coil to be $2Wb$.

Hence, option A is found to be the correct answer.

Note:
Let us just recall that the electromotive force developed as the resultant of the change in magnetic flux opposes the same change in magnetic flux which produced it as per Lenz’s law. This law is based on conservation of energy. Also, the magnetic flux is the measure of the strength of the magnetic field in a given area.