Question

In a club of 70 members 30 play tennis but not cricket and 55 play tennis. How many members play cricket but not tennis? (Each member plays either tennis or cricket).
A. $15$
B. $20$
C. $30$
D. $40$

Answer 1

According to the question given in the question we have to determine the number of members that play cricket but not tennis when in a club of $70$ members $30$ play tennis but not cricket and 55 play tennis. So, first of all we have to determine the Venn-diagram for each of the members who play tennis or cricket or both of the games.
Now, we have to determine the number of members that play both of the games which are as mentioned in the question are tennis and cricket with the help of the Venn-diagram in which the members will be common for both and can be treated as the members who play both of the games.
Now, we have to determine the number of members who plays only cricket and not tennis which can be again determined with the help of Venn-diagram in which we have to take the members who only plays cricket by subtracting the members who plays tennis and both of the games tennis and cricket by the total number of members who plays all of the games.

Complete step by step answer:
Step 1: First of all we have to determine the Venn-diagram for all of the cases in which the members who play cricket and the members who play tennis and the members who plays tennis and cricket both of the games which is as below:

Step 2: Now, we have to determine the number of members who plays both of the games tennis and cricket with the help of the Venn-diagram as we have obtained in the solution step 1 hence, we have to subtract the members who plays cricket by the number of players who play tennis but not cricket. Hence,
$\Rightarrow$Number of members who play both of the games:
$\Rightarrow 55 - 30 = 25$
We can also understand it with the help of the diagram as below:

Step 3: Now, we have to determine the number of members who plays only cricket and not tennis which can be again determined with the help of Venn-diagram in which we have to take the members who only plays cricket by subtracting the members who plays tennis and both of the games tennis and cricket by the total number of members who plays all of the games as mentioned in the solution hint.
$\Rightarrow$Number of members who plays cricket but not tennis:
$\Rightarrow 70 - 25 - 30 = 15$
We can also understand it with the help of the diagram as mentioned below:

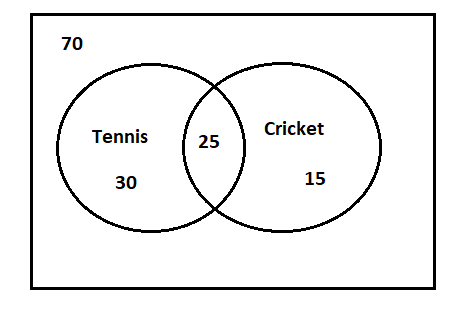
Hence, with the help of the Venn-diagram we have obtained the number of members who play only cricket but not tennis is 15. Therefore option (A) is correct.

Note: To determine the number of members who play cricket but not tennis it is necessary that first of all we have to determine the number of members who play both of the games cricket and tennis.
The Venn-diagram helps to explain the number of members that helps to determine how many members of the given two games.