Question

In a class of sixty students, 30 read Hindi, 35 read English newspapers. Then the number of students who read both papers are
A. 5
B. 30
C. 425
D. 60

Answer 1

Hint: In the above question first of all we will suppose the number of students who read Hindi and English to be variable and then we will use the formula of set theory given as below,
$n\left( {A \cap B} \right) = n\left( A \right) + n\left( B \right) - n\left( {A \cup B} \right)$
Where, n (A) and n (B) are two sets,
$n\left( {A \cap B} \right)$ means n (A) and n (B) (common).
$n\left( {A \cup B} \right)$ means n (A) or n (B).

Complete step-by-step answer:
We have been given that in a class of 60 students, 30 read Hindi, 35 read English newspapers, then, we have to find the number of students who read both papers.
Let the number of students who read Hindi is n (A) and the number of students who read English is n (B).
Then, we have,
${\text{n}}\left( {\text{A}} \right) = {\text{3}}0$
${\text{n}}\left( {\text{B}} \right) = {\text{35}}$
Student read Hindi or English $= n\left( {A \cup B} \right) = 60$
Student read Hindi and English $= n\left( {A \cap B} \right)$
We know that according to set theory,
$\begin{array}{l}n\left( {A \cap B} \right) = n\left( A \right) + n\left( B \right) - n\left( {A \cup B} \right)\\\n\left( {A \cap B} \right) = 30 + 35 - 60\\\n\left( {A \cap B} \right) = 65 - 60\\\n\left( {A \cap B} \right) = 5\end{array}$
Hence, students who read both English and Hindi are equal to 5.
Venn diagram:

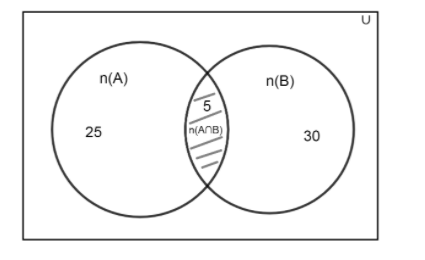
Here, n (A) is the number of students who read Hindi, n (B) is the number of students who read English and $n\left( {A \cap B} \right)$ means the number of students who read Hindi and English both.
Therefore, the correct option is A.

Note: It is important to understand the meaning of $'\, \cup '$ i.e. union and $' \cap '$ i.e. intersection, if the two statement is joined by ‘and’ then we use union and if the two statement is joined by ‘or’ then we use intersection. Most often students have this misconception that $n\left( {A \cap B} \right)$ contains elements common to n (A) and n (B), so they write the formula as $n\left( {A \cap B} \right) = n\left( A \right) + n\left( B \right)$. But this is wrong, because this represents all the elements in A and B and the elements repeating must be deducted.