Question
Question: In a class of 60 students, 25 students play cricket, 20 students play tennis and 10 students play bo...
In a class of 60 students, 25 students play cricket, 20 students play tennis and 10 students play both the games, then the number of students who play neither are
(a). 0
(b). 35
(c). 45
(d). 25
Solution
Hint: Find the number of students who play both cricket and tennis by finding n(A∪B). From this the students who play neither cricket nor tennis can be formed by subtracting from total students.
Complete step-by-step answer:
Given the total number of students in a class = 60.
Let ‘A’ be the set of students who play cricket, which is 25 in number.
∴n(A)=25
Let ‘B’ be the set of students who play tennis, 20 in number.
∴n(B)=20
The number of students who play both cricket and tennis is 10.
∴n(A∩B)=10
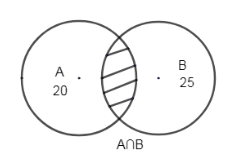
The shaded area shows A∩B.
The intersection of two sets A and B, consist of all elements that are both in A and B. The figure shows a Venn diagram representing the same.
Here, we are asked to find the number of students who don’t play cricket or tennis. Thus we need to find (A∪B) and subtract it from the total number of students.
A∪B is A union B, which means creating a new set containing every element from either of A and B.
The given Venn diagram represents A∪B.
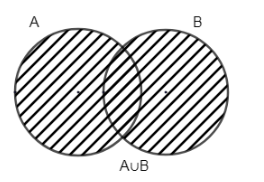
Hence, n(A∪B)=n(A)+n(B)−n(A∩B)
This formula can be directly derived from the above Venn diagram,
∴n(A∪B)=25+20−10=35.
Here, 35 students play at least one out of cricket or tennis out of 60 students in a class.
∴The number of students who play neither cricket nor tennis =
Total students – number of students who play at least one game
= Total students - n(A∪B)
= 60 – 35 = 25
∴The number of students who play neither cricket nor tennis = 25.
Hence, option (d) is the correct answer.
Note: A Venn diagram is used to represent all possible relations of different sets. Here we used A∩B, which is the intersection of 2 sets to represent the common elements in both set A and B. And A∪Brepresents the combined elements of set A and B.
Care should be taken not to confuse between A∩B and A∪B.
