Question

In a class of 60 students. 23 play hockey, 15 play basketball, and 20 play cricket, 7 play hockey and basketball, 5 play cricket and basketball, 4 play hockey and cricket and 15 students do not play any of these games. Then

1. 4 play hockey, basketball and cricket
2. 20 play hockey but not cricket
3. 1 play hockey and cricket but not basketball
4. all above are correct

Answer 1

23 students of hockey are the students who plays hockey only , hockey and cricket only and they are those also who plays hockey and basketball only as well as those who plays hockey + basketball + cricket it all means that these 23 students are the total students who plays hockey doesn’t matter they play other games or not but they play hockey. And similarly the students of basketball and cricket are also the total students of each game.

Complete step by step answer :
We know that the total number of students in the is class is 60 but out of these 60 students 15 students do not play any of the games so now only 60 – 15 = 45 students play the games.
Let us now do this question with the help of Venn diagram.

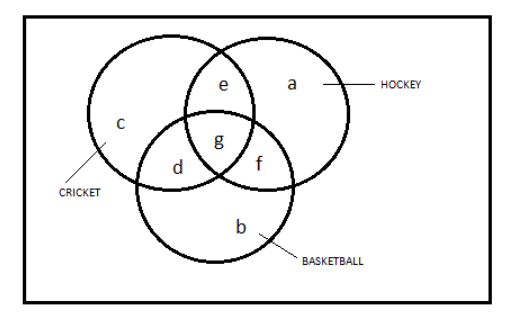
Now as given in question
a + e + g + f = 23 ( total hockey ) ( 1 )
b + d + g + f = 15 ( total basketball ) ( 2 )
c + e + g + d = 20 ( total cricket ) ( 3 )
And as it is also given that
e + g = 4 ( cricket and hockey )
f + g = 7 ( hockey and basketball )
d + g = 5 ( cricket and basketball )
Now a + b + c + d + e + f + g = total number of students that play any of the games
a + b + c + d + e + f + g = 60 – 15 = 45 students
Now by putting the value of f + g = 7 in equation ( 1 ) we get a + e = 23 – 7 = 16 and by putting the value of d + g = 5 in equation ( 3 ) we will get c + e = 15.
And similarly by following the substitution method we will get
b + d = 8 , b + f = 10 , c + d = 16 , and also we get b + c + d = 22, a + c + e = 30 and a + b + f=25
and from by solving all the above equations by putting the value of all the equations we will get
b = 6
a = 15
c = 14
e = 1
d = 2
f = 4 and g = 3
And from all the above values we come to know that as e ( i.e. students who play hockey and cricket only = 1 )
Hence C is the correct option.

Note: Whenever we come up with such types of problems we must figure out the given statement into a Venn diagram because it becomes very easy to solve the equation according to the Venn diagram. And solving equations with a substitution method is the best and easiest way to solve the equations with various variables.