Question

In a class of 50 students it was found that 27 study History, 27 study civics, 25 study economics, 15 study both history and civics, 16 study both civics and economics, 14 study both history and economics, 9 study all the three subjects. Find:

1. How many study economics only
2. How many students do not study any of the three subjects
3. How many study economics but not civics.

Answer 1

Find the number of students who do economics only by no of students who take economics and subtract the no: of students who do other subjects along with other subjects. To find students who don't do the 3 subjects then subtract the no: of students who do these subjects from the total no: of students. Similarly find the other cases.

Complete step by step solution:
The total no. of students in the class =50.
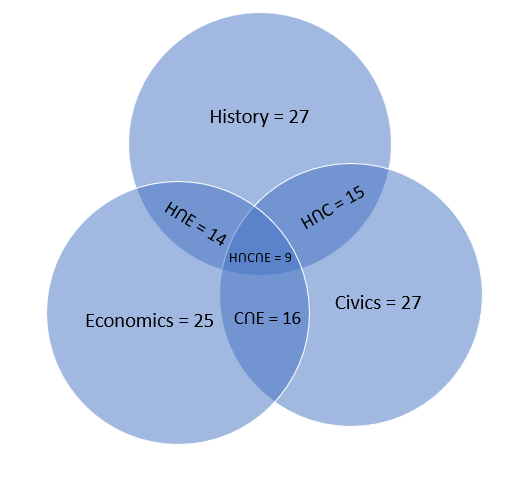
Let us take History civics, and economics as H,C & E.
The no. of students who study history $=n\left( H \right)=27$ .
The no. of students who study civics $=n\left( C \right)=27$ .
The no. of students who study economics $=n\left( E \right)=25$ .
The no. of students who study both history and civics $=n\left( H\cap C \right)=15$ .
The no. of students who study both civics and economics $=n\left( C\cap E \right)=16$ .
The no. of students who study both history and economics $=n\left( H\cap E \right)=14$.
The no. of students who learn all 3 subjects $=n\left( H\cap C\cap E \right)=9$ .

1. First we need to find the no. of students who learn economics only. The no. of students who learn only economics $=n\left( E \right)-n\left( H\cap E \right)-n\left( C\cap E \right)-n\left( H\cap C\cap E \right)$ .
   Substitute the values in the above expression .To get the no. of students who studies economics alone, you need to subtract the combined study of $n\left( H\cap E \right)$ and $n\left( C\cap E \right)$ from $n\left( E \right)$ .
   $\therefore$ The no. of students who learn economics alone =4.
2. Now we need to find the no. Of students who don't study any of the 3 subjects.
   No. of students who don't study 3 subjects = Total students – total no. of students learning the subjects.
   $=\text{total students }-n\left( H\cup C\cup E \right)$ .
   $n\left( H\cup C\cup E \right)=n\left( H \right)+n\left( C \right)+n\left( E \right)-n\left( H\cap C \right)-n\left( C\cap E \right)-n\left( H\cap E \right)+n\left( H\cap C\cap E \right)$
   Let us substitute all the values in the above expression.
   $\begin{aligned} & n\left( H\cup C\cup E \right)=27+27+25-15-16-14+9 \\\ & =88-45=43 \\\ \end{aligned}$
   $\therefore$ Total no. of students who learn the subjects =43.
   $\therefore$The no. of students who doesn’t study the 3 subjects $\text{= total students }-n\left( H\cup C\cup E \right)=50-43=7$ .
   $\therefore$7 students doesn’t study any of the 3 subjects.
3. Now we need to find the no. of students who study economics but not civics
   The students who study economics but not civics $=\text{No}\text{. of students who learn only economics }+n\left( H\cap C \right)-n\left( H\cap C\cap E \right)$
   Now substitutes a;; the value in the above equation.
   Economic but not civics $=4+14-9=9$ .

1) No. of students who study economics only =4
2) No. of students who don’t study any of the three subjects =7.
3) No. of students who learn economics but not civics =9.

Note: we can also solve this problem using a venn diagram. With the help of a venn diagram you can find the quantities like the union and intersection of different subjects. It is just the pictorial relationship among 2 or more sets.