Question

In a class of 50 students, each of the students passed either in mathematics or in science or in both. 10 students passed in both and 28 passed in science. Find how many students passed in mathematics.

Answer 1

For solving this question, we will visualize the vennn diagram initially and then using the given data find the number of students completely passed in mathematics.
Let us now discuss about Venn diagram.
VENN DIAGRAM: A Venn diagram is a diagram that shows all possible logical relations between finite collections of different sets.

Complete step by step answer:
As mentioned in the question, the total number of students is 50 and the number of students that passed in both the subjects, mathematics and science are 10. The venn diagram can be visualized as follows:

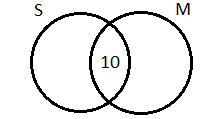
Now, we know that the total number of students that passed in science is 28.
From this we will get the number of students that passed only in science is (28 – 10), i.e. 18.

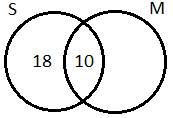
Therefore, the number of students that passed in mathematics only will be
[Total number of students – (Students that passed in science + Students that passed in both the subjects)]
So, the number of students that passed in mathematics is [50 – (18 + 10)] = [50 – 28] = 22.
Hence, the answer of this question is 22, i.e. the number of students that passed only in mathematics is 22.

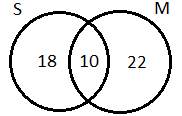
Hence, the total number of students passed in mathematics is
= [total number of students passed in mathematics only]+ [ total number of students passed in both the subjects]
$\Rightarrow 22+10$
= 32

Hence, the total number of students passed in mathematics is 32.

Note: It is very important to do all the calculations very carefully as if there is any mistake in the calculation; the answer we will conclude out can be wrong. Here, we should take care that in the question it is asked for the total number of students passed in mathematics not the number of students passed in mathematics only.