Question

In a class of 45 students 22 can speak Hindi only 12 can speak English only. The number of students who can speak both Hindi and English is
A) $11$
B) $23$
C) $33$
D) $34$

Answer 1

We can solve the problem by using the general relations and using the Venn diagram.
We will apply the formula of $n(H \cup E) = n(H) + n(E) + n(H \cap E)$. Here, $H$ means number of students who can speak Hindi and $E$ means the number of students who can speak English.
Then, using the formula and given information we can find the number of students who can speak both.

Complete step by step answer:
It is given that; the total number of students in the class is $45$.
The number of students who can speak Hindi is $22$.
The number of students who can speak English is $12$.
We have to find the number of students who can speak both Hindi and English.
So, as per the given information
$n(H \cup E) = 45$
$n(H) = 22$
$n(E) = 12$
Let us consider the number of students who can speak both Hindi and English is $x$ that is $n(H \cap E) = x$.
We have to find the value of $n(H \cap E)$.
We know that,
$\Rightarrow n(H \cup E) = n(H) + n(E) + n(H \cap E)$
Substitute the values in the above formula we get,
$\Rightarrow 45 = 22 + 12 + x$
Simplifying we get,
$\Rightarrow x = 11$
Hence, the number of students who can speak both Hindi and English is $11$.

$\therefore$ The correct answer is option A) $11$

Note:
We can solve the sum by using a Venn diagram.

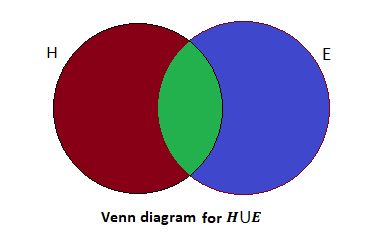
Here, the red shaded part indicates the number of students who can speak Hindi is $22$.
The blue shaded part indicates the number of students who can speak English is $12$.
The green shaded part indicates the number of students who can speak both Hindi and English.
The total number of students in the class is $45$.
We have to find the value of the green shaded part.
So, the value of green-shaded part is
$45 - (22 + 12) = 11$
Hence, the number of students who can speak both Hindi and English is $11$.