Question

In a class of $120$ students, $30$ study Maths, $40$ study Physics, $45$ study Chemistry, $15$ study Math and Physics, $20$ study Physics and Chemistry, $12$ study Math and Chemistry and $8$ study all the three. How many are
a.Studying at least one of these subjects
b.did not study any of these
c.how many take only one subject
d.how many study exactly $2$ of the three subjects

Answer 1

We use a Venn diagram to describe the given relations of the different sets. A close figure is used for each set and we generally use circles to denote the set.
Here, we are asked four questions based on the given information. First, let us draw a Venn diagram so that it can be easy to solve.

Complete step by step answer:
Let M be Mathematics, P be Physics and C be Chemistry.
We are given the following information.
It is given that the number of students who study Mathematics is $n\left( M \right) = 30$
The number of students who study Physics is given as $n\left( P \right) = 40$
The number of students who study Chemistry is given as $n\left( C \right) = 45$
The number of students who study both Mathematics and Physics is given as $n\left( {M \cap P} \right) = 15$
The number of students who study both Physics and Chemistry is given as $n\left( {P \cap C} \right) = 20$
The number of students who study both Mathematics and Chemistry is given as $n\left( {M \cap C} \right) = 12$
It is given that the number of students who study all the three subjects is $n\left( {M \cap P \cap C} \right) = 8$
The above information is described in Venn diagram as shown.

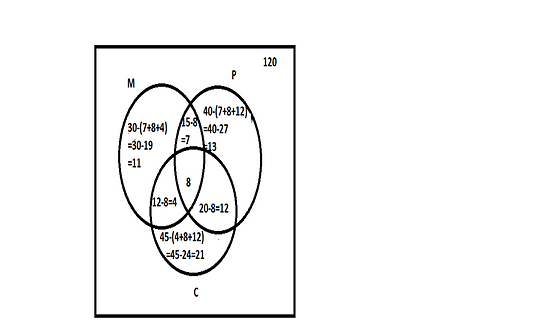
a) We are asked to calculate the number of students who study at least one of these subjects.
Here we need to add all the values that we have found.
From the above Venn diagram, the number of students who study at least one of three subjects
$= 11 + 13 + 21 + 7 + 4 + 12 + 8$
$= 76$
b) We are asked to calculate the number of students who study did not study any of these.
From the above Venn diagram, the number of students who study did not study any of these $= total{\text{ }}number{\text{ }}of{\text{ }}students - \left( {11 + 13 + 21 + 7 + 4 + 12 + 8} \right)$ $= 120 - 76$
$= 44$
c) We are asked to calculate the number of students who study only one subject.
From the above Venn diagram, the number of students who study only one subject
$= 11 + 13 + 21$
$= 45$
d) We are asked to calculate the number of students who study exactly two of the three subjects.
From the above Venn diagram, the number of students who study exactly two of the three subjects $= 7 + 4 + 12$
$= 23$

Note:
First, we should gather the information about the universal set from the given question.
A universal set is a total value and we usually draw the universal set in the rectangle in a Venn diagram. Circles denote the different sets that are given in the question.