Question

In a class, 40% of the students participated in the Mathematics quiz, 30% in the Science quiz, and 10% in both the quiz programs. If a student is selected at random from the class, find the probability that the student participated in Mathematics or Science or both quiz programs
a)$\dfrac{2}{5}$
b) $\dfrac{3}{5}$
c) $\dfrac{3}{7}$
d)None of these

Answer 1

Let us assume that the total number of students is 100. We know that $40\%$ of the students participated in the Mathematics quiz, $30\%$ in the Science quiz, and $10\%$ in both the quiz programs. Find the number of students participating in different quizzes. Find the probability for each case by using the probability formula: $P=\dfrac{\text{possible outcomes}}{\text{total outcomes}}$, then for finding the probability of selecting a student who participated in any of the quizzes we will use : $P\left( A\cup B \right)=P\left( A \right)+P\left( B \right)-P\left( A\cap B \right)$

Complete step-by-step solution:

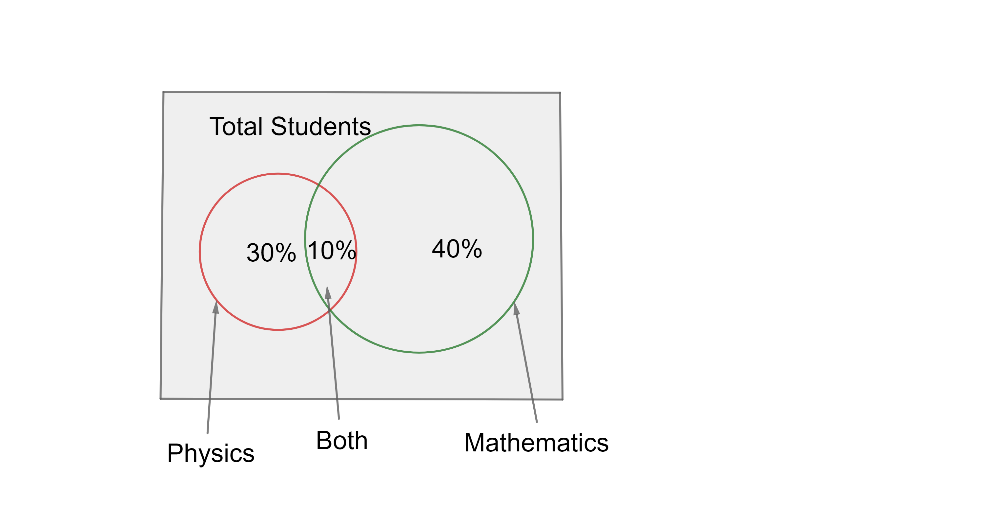
The above Venn diagram shows the representation of students who participated in the Mathematics quiz or science quiz or both.
As we have assumed that the total number of students is 100
So, the number of students who participated in the Mathematics quiz is $40\%$, i.e.

& =\dfrac{40}{100}\times 100 \\\ & =40 \\\ \end{aligned}$$ Let the probability that the student participated in Mathematics quiz be $P\left( A \right)$ , now we know that $P=\dfrac{\text{possible outcomes}}{\text{total outcomes}}$ , therefore : $P\left( A \right)=\dfrac{\text{No}\text{. of students participated in maths quiz}}{\text{Total number of students}}=\dfrac{40}{100}=\dfrac{4}{10}\text{ }.......\text{Equation 1}$ Similarly, the number of students who participated in the Science quiz is $30\%$, i.e. $$\begin{aligned} & =\dfrac{30}{100}\times 100 \\\ & =30 \\\ \end{aligned}$$ So let, the probability that the student participated in Science quiz be $P\left( B \right)$ , now we know that $P=\dfrac{\text{possible outcomes}}{\text{total outcomes}}$ , therefore : $P\left( B \right)=\dfrac{\text{No}\text{. of students participated in science quiz}}{\text{Total number of students}}=\dfrac{30}{100}=\dfrac{3}{10}\text{ }.......\text{Equation 2}$ Similarly, the number of students who participated in both quizzes is $10\%$, i.e. $$\begin{aligned} & =\dfrac{10}{100}\times 100 \\\ & =10 \\\ \end{aligned}$$ Now, let the probability that the student participated in both quizzes will be $P\left( A\cap B \right)$ , now we know that $P=\dfrac{\text{possible outcomes}}{\text{total outcomes}}$ , therefore : $P\left( A\cap B \right)=\dfrac{\text{No}\text{. of students participated in both the quizzes}}{\text{Total number of students}}=\dfrac{10}{100}=\dfrac{1}{10}\text{ }.......\text{Equation 3}$ So, the probability of selecting a student who participated in any of the quizzes will be: $P\left( A\cup B \right)$ Now we know that: $P\left( A\cup B \right)=P\left( A \right)+P\left( B \right)-P\left( A\cap B \right)$ We will put the values from equation 1, 2 and 3: Therefore, $P\left( A\cup B \right)=\dfrac{4}{10}+\dfrac{3}{10}-\dfrac{1}{10}=\dfrac{6}{10}=\dfrac{3}{5}$ **Hence, option (b) is the correct answer.** **Note:** The formula $P\left( A\cup B \right)=P\left( A \right)+P\left( B \right)-P\left( A\cap B \right)$ is also known as de morgan’s law and is derived by using the set theory. In these kind of questions that is of probability, always explain in detail about the steps that you are using so that examiner have a better understanding of your solutions.