Question

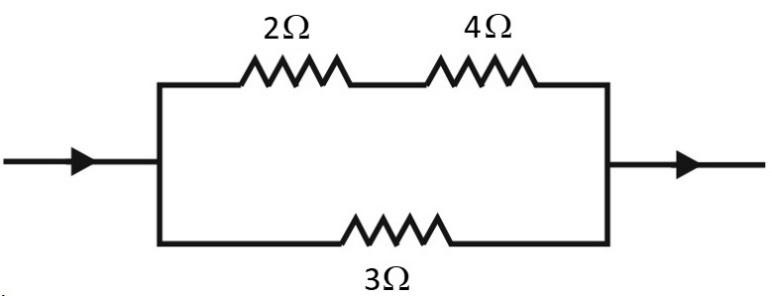
In a circuit shown in figure, the heat produced in $3$ ohm resistor due to a current flowing in it is $12J$. The heat produced in $4$ ohm resistor is

A) $2J$
B) $4J$
C) $64J$
D) $32J$

Answer 1

When the current flow on the resistor then energy is developed in the form of Heat and it is equal to$H = {i^2}Rt$. Also as in series current is same so the current through 2 ohm and 4 ohm resistor will be the same.

Complete step by step answer:
We know that Heat energy generated is given by$H = {i^2}Rt$,
H $=$ Heat Energy
I $=$ Current
R $=$ Resistor
t $=$ time
For $3\Omega$ resistance heat $= \dfrac{{{V^2}}}{R} = 12J$
$\Rightarrow {v^2} = 12 \times R \\\ \Rightarrow {v^2} = 12 \times 3 \\\ \Rightarrow {v^2} = 36 \\\ \Rightarrow v = \sqrt {36} \\\ \Rightarrow v = 6 \\\$
So, potential difference in $3\Omega$resistor $= 6\,volt$
For upper branch in parallel combination
Here, $2\Omega$and $4\Omega$are in series combination
Rnet$= 2 + 4 = 6\Omega$
Now, potential difference of upper branch $= 6\,volt$
From Ohm’s Law:
$i = \dfrac{V}{{{R_{net}}}} = \dfrac{6}{6} = 1\,Amp$
So, the upper branch current (i) $= \;1\,Amp$is flown.
So, Heat produced in $4\Omega \; = \;{i^2}\,Rt$
$H = 1 \times 1 \times 4 \times 1\;\;\;[9\,F\,t = 1\,\sec ]$
$\boxed{H = 4J}$

So, the correct answer is “Option B”.

Additional Information:

1. You should have known the concept of combination of resistances. Here series combination is applied.
   $\boxed{{R_{net}} = {R_1} + {R_2}}$
2. In parallel, potential differences will be the same for different branches.
3. Concept of heat energy applied.

Note:

1. $\dfrac{H}{t} = {i^2}R = \dfrac{{V{}^2}}{R}$is applied
2. Concept of series combination is applied (Rnet $= {R_1} + {R_2})$
3. Proper using the concept question will be solved.