Question

In a circuit L,C and R are connected in series with an alternating voltage source of frequency f. The current leads the voltage by ${{45}^{\circ }}$. The value of c is,
$\begin{aligned} & \left( A \right)\dfrac{1}{\pi f\left( 2\pi fL-R \right)} \\\ & \left( B \right)\dfrac{1}{2\pi f\left( 2\pi fL-R \right)} \\\ & \left( C \right)\dfrac{1}{\pi f\left( 2\pi fL+R \right)} \\\ & \left( D \right)\dfrac{1}{2\pi f\left( 2\pi fL+R \right)} \\\ \end{aligned}$

Answer 1

First find the nature of the circuit. Here the circuit is capacitive. The tan of the angle is the ratio of the difference between capacitive reactance and inductive reactance to the resistance. Where inductive reactance is the product of inductance and angular frequency. Similarly, capacitive reactance is the product of capacitance and angular frequency. By substituting these values and substituting we get the value of capacitance.

Complete step by step solution:

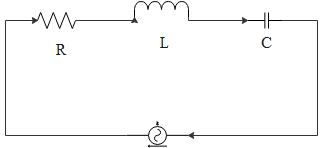
The circuit is capacitive. Thus,
${{X}_{C}}\rangle {{X}_{L}}$
$\phi ={{45}^{\circ }}$
$\tan \phi =\dfrac{{{X}_{C}}-{{X}_{L}}}{R}$
$\tan {{45}^{\circ }}=1$
$\Rightarrow {{X}_{C}}-{{X}_{L}}=R$
$\Rightarrow {{X}_{C}}=R+{{X}_{L}}$
Inductive reactance, ${{X}_{L}}=\omega L=2\pi fL$
$\dfrac{1}{\omega c}=\dfrac{1}{\omega \left( \omega L+R \right)}$
$\Rightarrow c=\dfrac{1}{\omega \left( \omega L+R \right)}$
where, $\omega =2\pi f$
$\therefore c=\dfrac{1}{2\pi f\left( 2\pi fL+R \right)}$
Hence, option (D) is correct.
Phasor diagram,

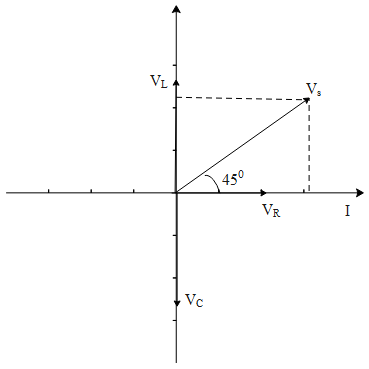
So, the correct answer is “Option D”.

Additional Information: Inductive reactance is the name given to a changing current flow. The impedance is usually measured in ohms, just like resistance. That is, the inductive reactance has the same unit of resistance. Capacitive reactance decreases with the increasing value of AC frequency, while inductive reactance increases with increasing AC frequency. When current passes through a coil, then it will become electromagnetic. The current that flows through the coil will have an opposition like resistance upon its inductance and frequency waveform. Where inductive reactance is the product of inductance and angular frequency. Similarly, capacitive reactance is the product of capacitance and angular frequency. By substituting these values and substituting we get the value of capacitance.

Note: Also the inductive reactance has the same unit of resistance. That is, both are measured in ohms. The inductive reactance is proportional to the angular frequency of AC voltage source. Where inductive reactance is the product of inductance and angular frequency. Similarly, capacitive reactance is the product of capacitance and angular frequency. By substituting these values and substituting we get the value of capacitance.