Question

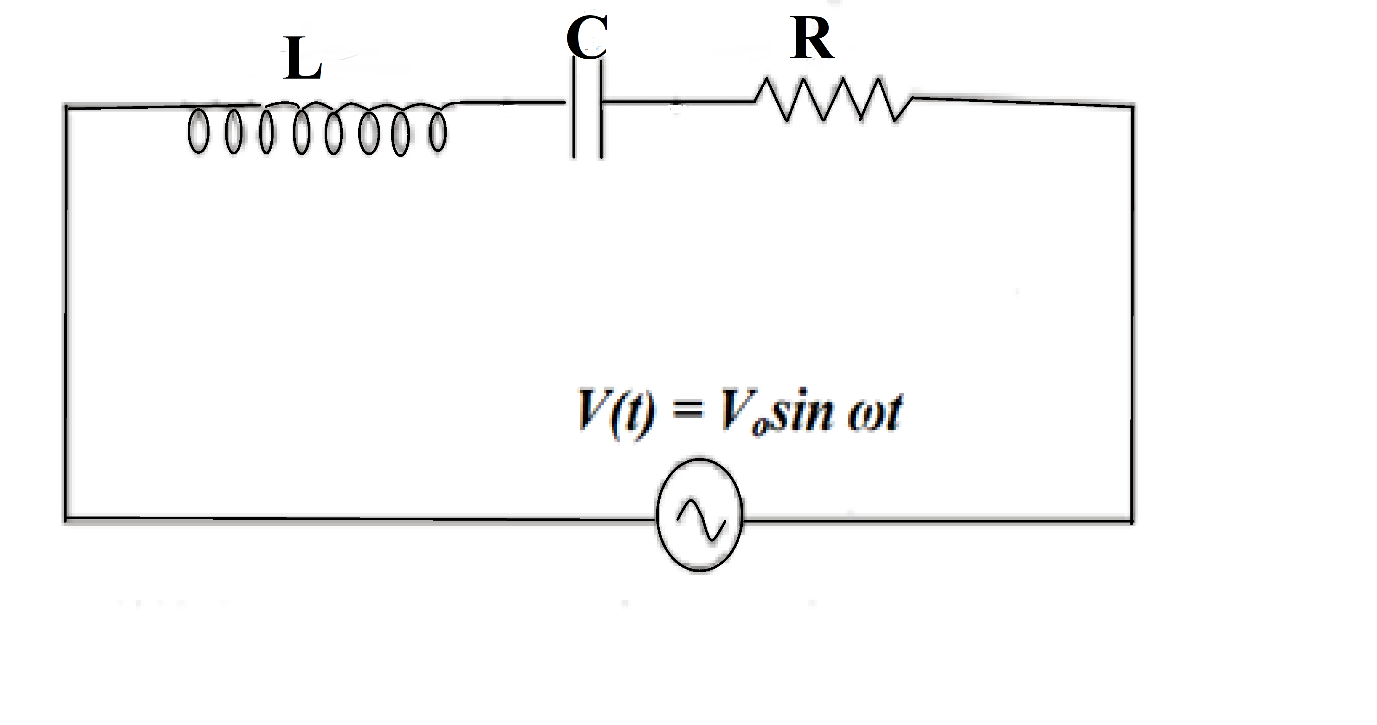
In a circuit L, C and R are connected in series with an alternating voltage source of frequency f. The current leads the voltage by ${{45}^{\circ }}$. The value of C is:
A. $\dfrac{1}{\pi f(2\pi fL+R)}$
B. $\dfrac{1}{\pi f(2\pi fL-R)}$
C. $\dfrac{1}{2\pi f(2\pi fL+R)}$
D. $\dfrac{1}{2\pi f(2\pi fL-R)}$

Answer 1

In this question, we can use the help of the relation between Capacitive Resistance (${{X}_{C}}$) and Inductive Resistance (${{X}_{L}}$). A calculation of the resistance of a capacitor to AC (alternating current) is capacitive reactance. Inductive reactance is the name assigned to a shifting current flow to the opposition. Much like resistance, this impedance is measured in ohms,

Formula used:
For solving this question, we will be using
$\tan \phi =\dfrac{{{X}_{L}}-{{X}_{C}}}{R}$

Complete step by step answer:
Before solving the question, let us take a look at all the given parameters

$\phi ={{45}^{\circ }}$
${{X}_{L}}=2\pi fL$
${{X}_{C}}=\dfrac{1}{2\pi fC}$
Now, using the above values
We have,
$\tan {{45}^{\circ }}=\dfrac{{{X}_{L}}-{{X}_{C}}}{R}$
$\Rightarrow 1=\dfrac{{{X}_{L}}-{{X}_{C}}}{R}$
$\Rightarrow {{X}_{C}}={{X}_{L}}-R$
$\Rightarrow \dfrac{1}{2\pi fC}=2\pi fL-R$
$\Rightarrow 2\pi fC=\dfrac{1}{2\pi fL-R}$
$\Rightarrow C=\dfrac{1}{2\pi f(2\pi fL-R)}$
So, the correct answer to this question is $C=\dfrac{1}{2\pi f(2\pi fL-R)}$, i.e., Option D

Note:
In the above question, an LCR circuit has been discussed. An electrical circuit consisting of an inductor ( L), capacitor (C) and resistor (R) connected in series or parallel is an LCR circuit, also known as a resonant circuit, tuned circuit, or an RLC circuit. In terms of Phasors, the LCR circuit analysis can be best understood.