Question

In a children’s park there is a slide, which has a total length of 10m and a height of 8m. A vertical ladder is attached to the top of the slide. A child of mass 20kg slides down to the ground. The average friction offered by the slide is three-tenth of his weight. The work done by the slide on the boy as he comes down is:

A). 0 J
B). +600 J
C). -600 J
D). +1600 J

Answer 1

Note that the only influencing force on the boy contributed by the slide is the frictional force between the boy and the surface of the slide. This force is usually proportional to the normal reaction force acting on the boy, but since we are given that the value of this force is three-tenths of the gravitational force acting on the boy we assume the same and calculate the frictional force that impedes the motion of the boy down the slide. Therefore, the work done by the slide on the boy is this frictional force acting along the length of the slide. Use this to quantitatively determine the work done.
Formula Used: Frictional force: $F_r = \mu N$
Work done: $W = \vec{F}.\vec{s}$

Complete step-by-step solution:
Let us begin by drawing a diagram that represents the influencing forces resolved into their directional components.
We are given that the mass of the child is $m=20\;kg$. This means that the gravitational force acting on the child is $F_{g} = mg = 20 \times 10 = 200\;N$, assuming the acceleration due to gravity $g \approx 10\;ms^{-2}$.

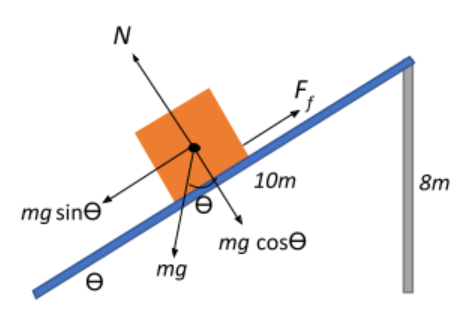
Now, the force offered by the slide is only the frictional force that impedes the motion of the boy as he slides down the incline. Therefore, the work done by the slide is in imparting friction to the motion of the boy.
$W = -F_{f}.s$, where s is the displacement of the boy over the slide which is nothing but the length of the slide $s = 10\;m$.
Now, we are given that the frictional force is three-tenths of his weight.
$\Rightarrow F_{f} = \dfrac{3}{10} \times F_{g} = \dfrac{3}{10} \times 200 = 60\;N$
In this case, the work done by the slide on the boy as he comes down is given as:
$W = -F_{f}.s = -60 \times 10 = -600\;J$
Therefore, the correct choice is C. -600 J

Note: It is very important to remember to separate the components of forces and choose the correctly contributing component for each direction. Also, do not forget to include the coefficient of friction while determining the frictional force in case it is explicitly mentioned. It is also crucial to remember the sign convention for work done. If any force retards the motion of a body, the work done by that force will be negative but if a force contributes to the motion of the body the work done by that force will be positive.