Question

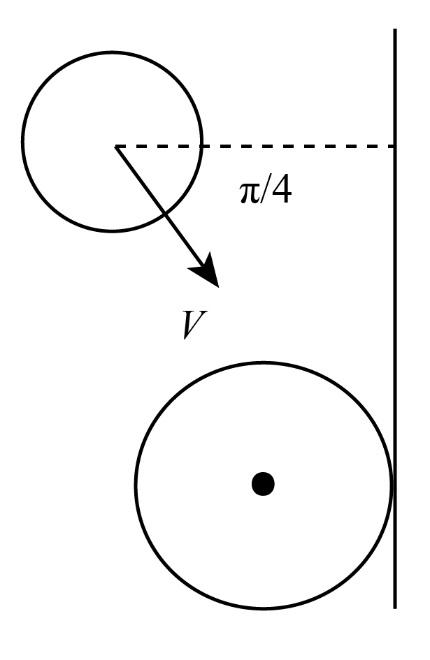
In a carrom-board game the striker and the coins are identical and of mass m. In a particular hit the coin is hit when it is placed close to the edge of the board as shown in the figure such that the coin travels parallel to the edge. If the striker is moving with speed v before strike, then the net impulse on the striker during collision of it moves perpendicular to the edge is (assume all collisions to be perfectly elastic).

(A) $mv\sqrt {\dfrac{5}{2}}$
(B) 2mv
(C) $\dfrac{{mv\sqrt 3 }}{2}$
(D) mv

Answer 1

This question uses the concept of conservation of linear momentum and impulse. You need first to calculate the component of velocity of the striker in the horizontal and vertical direction. Then you need to calculate the change in impulse in both the directions. Later, you can calculate net impulse by a change in impulse in the horizontal direction and vertical direction.

Complete step by step answer:
In the question it is given that, the mass of the striker and the coin is m. The speed of the striker, before it strikes the coin is v. Also, it is mentioned that the collision is a perfectly elastic collision.

As we know, in the case of perfectly elastic collision, $e = 1$.
The x-component of speed of the striker is given as ${v_x} = v\cos 45^\circ$ and the y-component of the speed of the striker is given as ${v_y} = v\sin 45^\circ$.

On applying the conservation of linear momentum along the x-axis, we get,
\begin{array} mv\cos 45^\circ = - mv'\\\ v' = \dfrac{v}{{\sqrt 2 }} \end{array}

Similarly, on applying the conservation of linear momentum along the y-axis, we get,
\begin{array} mv\sin 45^\circ = 0\\\ v = 0 \end{array}

This means that there is no motion along the y-direction.

The change in impulse of the striker along the x-axis can be given as,
\begin{array} \Delta {I_x} = \dfrac{{mv}}{{\sqrt 2 }} - \left( { - \dfrac{{mv}}{{\sqrt 2 }}} \right)\\\ \Delta {I_x} = mv\sqrt 2 \end{array}

Similarly we can calculate the change in impulse of the striker along the y-axis as,
$\Delta {I_y} = \dfrac{{mv}}{{\sqrt 2 }}$

So we can calculate the net impulse on the striker as,
${I_{net}} = \sqrt {\Delta I_x^2 + \Delta I_y^2} \\\ \implies {I_{net}} = \sqrt {{{\left( {mv\sqrt 2 } \right)}^2} + {{\left( {\dfrac{{mv}}{{\sqrt 2 }}} \right)}^2}}$

On further solving the above expression,
${I_{net}} = \sqrt {{{\left( {mv\sqrt 2 } \right)}^2} + {{\left( {\dfrac{{mv}}{{\sqrt 2 }}} \right)}^2}} \ \implies {I_{net}} = mv\sqrt {2 + \dfrac{1}{2}} \\\ \implies {I_{net}} = mv\sqrt {\dfrac{5}{2}}$

Therefore, the net impulse of the striker during the collision is $mv\sqrt {\dfrac{5}{2}}$.

So, the correct answer is “Option A”.

Note:
You can make mistakes in the calculation part as it is very complex.
As it is mentioned in the question that, all the collisions are perfectly elastic, so the value of coefficient of restitution will be 1.
The component of velocity of the striker in the horizontal and vertical direction.