Solveeit Logo
Login

Question

Question: In a camp, each student played at least 2 games. The games were Scavenger Hunt, Animal Charades and ...

In a camp, each student played at least 2 games. The games were Scavenger Hunt, Animal Charades and Musical Chairs. Twelve students played all three games, 33 played the Scavenger Hunt, 29 played the Animal Charades and 36 played the Musical Chairs. How many students were there in the camp? $$$$

Explanation

Solution

We denote the number of students who played who played Scavenger Hunt as n(S)n\left( S \right), Animal Charades asn(A)n\left( A \right) and Musical Chairs as n(M)n\left( M \right). We find the number students in the camp n(S⋃A⋃M)=n(S)+n(A)+n(M)−3n(S⋂A⋂M)+n(S⋂A⋂M)n\left( S\bigcup A\bigcup M \right)=n\left( S \right)+n\left( A \right)+n\left( M \right)-3n\left( S\bigcap A\bigcap M \right)+n\left( S\bigcap A\bigcap M \right) where S⋂A⋂MS\bigcap A\bigcap M is the number of students who played all games.$$$$

Complete step-by-step answer:
We know that the number of elements in a set AA is represented as ∣A∣\left| A \right| or n(A)n\left( A \right). Let us denote the set of students who played Scavenger Hunt as $S$, Animal Charades as$A$ and Musical Chairs as $M$.
We are given in the question that 12 students played all three games. So we have;
n(S⋂A⋂M)=12n\left( S\bigcap A\bigcap M \right)=12
We are also given that 33 played the Scavenger Hunt, 29 played the Animal Charades and 36 played the Musical Chairs. So we have;
n(S)=33,n(A)=29,n(M)=36n\left( S \right)=33,n\left( A \right)=29,n\left( M \right)=36
We are asked in the question the number of students who were present in the camp which means n(S⋃A⋃M)n\left( S\bigcup A\bigcup M \right). We are not given the data of $n\left( S\bigcap A \right),n\left( A\bigcap M \right),n\left( M\bigcap S \right)$ which is the number of students who played both Scavenger Hunt and Animal Charades, Animal Charades and Musical Chairs, Musical Chairs and Scavenger Hunt respectively. We are only given, each student played at least 2 games which means $n\left( S\bigcap A \right),n\left( A\bigcap M \right),n\left( M\bigcap S \right)$ are non empty sets. Let us draw its Venn’ diagram

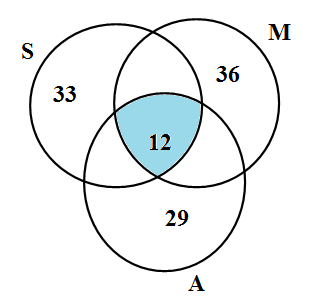
Let us consider the set S. We can write the union sets as
n(S⋃A⋃M)=n(S)+n(A)+n(M)−3n(S⋂A⋂M)+n(S⋂A⋂M)n\left( S\bigcup A\bigcup M \right)=n\left( S \right)+n\left( A \right)+n\left( M \right)-3n\left( S\bigcap A\bigcap M \right)+n\left( S\bigcap A\bigcap M \right)
The above relation comes from understanding that we are excluding the common intersection S⋂A⋂MS\bigcap A\bigcap M every time we take union two sets. So we put the values and get the total number of students in the camp as

& n\left( S\bigcup A\bigcup M \right)=n\left( S \right)+n\left( A \right)+n\left( M \right)-3n\left( S\bigcap A\bigcap M \right)+n\left( S\bigcap A\bigcap M \right) \\\ & \Rightarrow n\left( S\bigcup A\bigcup M \right)=33+29+36-3\times 12+12=74 \\\ \end{aligned}$$ **Note:** If there are three sets $A,B,C$ then the number of elements of their union set is given by $n\left( A\bigcup B\bigcup C \right)=n\left( A \right)+n\left( B \right)+n\left( C \right)-n\left( A\bigcap B \right)-n\left( B\bigcap C \right)-n\left( C\bigcap A \right)+n\left( A\bigcap B\bigcap C \right)$. We can derive the formula we used in our solution from this formula. We note that the number of elements in the set is cardinality or the cardinal number of the set.