Question

In a building programme the event that all the materials will be delivered at the correct time is M and the event that the building programme will be completed on time is F. Given that $P\left( M \right)=0.8$ and $P\left( M\cap F \right)=0.65$ , find $P\left( {F}/{M}\; \right)$ . If $P\left( F \right)=0.7$ , find the probability that the building programme will be completed on time if all the materials are not delivered at the correct time.
A . $P\left( {F}/{M}\; \right)=\dfrac{11}{16};P\left( {F}/{\overline{M}}\; \right)=\dfrac{1}{6}$
B . $P\left( {F}/{M}\; \right)=\dfrac{15}{16};P\left( {F}/{\overline{M}}\; \right)=\dfrac{1}{8}$
C . $P\left( {F}/{M}\; \right)=\dfrac{13}{16};P\left( {F}/{\overline{M}}\; \right)=\dfrac{1}{4}$
D . None of these.

Answer 1

Hint: At first find the value of $P\left( \text{M only} \right),P\left( \text{F only} \right)$ and $P\left( \text{neither M and F} \right)$by the given data to form the Venn diagram. Then use the identify $P\left( {A}/{B}\; \right)=\dfrac{P\left( A\cap B \right)}{P\left( B \right)}$ , where, A, B are events and with the help of Venn diagram we can solve it.

Complete step-by-step answer:
In this question we are said that in a building programme event all the materials will be completed on time is F.
So, we are given that $P\left( M \right)=0.8$ and $P\left( M\cap F \right)=0.65$
Here, $P\left( M \right)$ means probability of getting event ‘M’ occurred and $P\left( M\cap F \right)$ means probability of getting events for which both ‘M’ and ‘F’ will be considered. Also $P\left( F \right)$ means the probability of event ‘F’ occurring.
So, the probability of M only will be the difference of $P\left( M \right)$ and $P\left( M\cap F \right)$or $\left( 0.8-0.65 \right)$ or $0.15$ .
Hence $P\left( \text{M only} \right)$ is $0.15$ .
Now, we can similarly find the probability of F only by finding the difference of $P\left( F \right)$ and $P\left( M\cap F \right)$ or $\left( 0.7-0.65 \right)$ or $0.05$ . Hence, $P\left( \text{F only} \right)$ is $0.05$ .
Now we know that,
$\begin{aligned} & P\left( F \right)=0.7 \\\ & P\left( M \right)=0.8 \\\ & P\left( M\cap F \right)=0.65 \\\ & P\left( \text{F only} \right)=0.05 \\\ & P\left( \text{M only} \right)=0.15 \\\ \end{aligned}$
Which, we will represent in the Venn diagram.

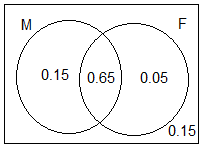
So from the Venn diagram we can find the probability of neither of the M and F as we know that the total sum of probability is 1.
So, the probability of neither M or F is $1-\left( 0.15+0.65+0.05 \right)$ or $0.15$ .
So now we will use the formula of conditional probability which is, if A and B are events then $P\left( {A}/{B}\; \right)=\dfrac{P\left( A\cap B \right)}{P\left( B \right)}$
So, here $P\left( {F}/{M}\; \right)$ can be written as $\dfrac{P\left( F\cap M \right)}{P\left( M \right)}$ so as we were given the value of $P\left( F\cap M \right)$ is 0.65 and $P\left( M \right)$ is $0.80$ . So the value of $P\left( {F}/{M}\; \right)$will be $\dfrac{0.65}{0.80}$ on simplifying we will get $\dfrac{3}{16}$ .
Now, we have to find the probability that the building program will be completed on time if all materials are not delivered at the correct time.
So in other words we have to find $P\left( {F}/{\overline{M}}\; \right)$ which can be evaluated using formula, $P\left( {A}/{B}\; \right)=\dfrac{P\left( A\cap B \right)}{P\left( B \right)}$.
So, $P\left( {F}/{\overline{M}}\; \right)=\dfrac{P\left( F\cap \overline{M} \right)}{P\left( \overline{M} \right)}$.
So, by the Venn diagram we can say that the value of $P\left( F\cap \overline{M} \right)$ is $0.05$ and $P\left( \overline{M} \right)$ is $1-\left( 0.65+0.15 \right)$ or $0.20$ .So the value of $P\left( {F}/{\overline{M}}\; \right)=\dfrac{0.05}{0.20}$or $\dfrac{1}{4}$.
Hence, the correct option is ‘C’.

Note: Students while solving for the Venn diagrams have confusions between event M and only M as even M also includes results of M and both M and F. These hold for F too. If a student takes P(M only) = 0.8, then it is not correct, so they have to be careful about such things while solving these types of questions. If they use such results, then it will affect the final result as well.