Question

In a board examination, $40$ students failed in physics, $40$ in chemistry and $35$ in math, $20$ failed in maths & physics, $17$ in physics and chemistry, $15$ in maths and chemistry and $5$ in all three subjects. If $350$ students appeared in the examination, how many of them did not fail in any subjects?

Answer 1

In this question, we have to work with the no. of students who do not fail in any exam. This question can be solved in two ways. First Venn diagram, draw three intersecting circles one for physics and remaining for math and chemistry. Write down the information & solve it out.
Another way, by using Set theory, i.e. Set formulae approach.

Complete step by step answer:
Venn Diagram:

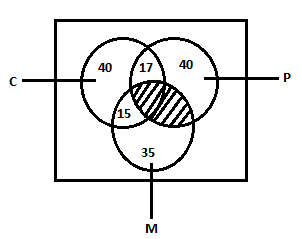
No. of students failed in every subject $= 5$.
No. of students failed in only Physics & chemistry$= 17 - 5 = 12$
No. of students failed in only chemistry & math’s$= 15 - 5 = 10$
No. of students failed in only maths & Physics$= 20 - 5 = 15$
$\therefore$No. of students failed in only math’s $= 35 - 10 - 15 - 5 = 5$
No. of students failed in only chemistry $= 40 - 15 - 5 - 17 = 3$
No. of students failed in only Physics$= 40 - 12 - 5 - 15 = 8$
$\therefore$Total no. of students failed $= 5 + 3 + 8 + 12 + 10 + 15 + 5 = 58$
$\therefore$ Total no. of students does not fail $= 350 - 58 = 292$
Since, total students $= 350$

Note:
We can solve this problem by using Set Formulae Approach also:
Consider, No. of students failed in Physics $= n\left( P \right) = 40$
No. of students failed in chemistry $= n\left( C \right) = 40$
No. of students failed in math’s $= n\left( M \right) = 35$
No. of students failed in Physics & chemistry $= n\left( {P \cap C} \right) = 17$
No. of students failed in chemistry & maths $= n\left( {C \cap M} \right) = 15$
No. of students failed in maths & Physics $= n\left( {M \cap P} \right) = 20$
No. of students failed in all subjects $= n\left( {M \cap P \cap C} \right) = 5$
Therefore, Total no. of students failed in at least on subject $= n\left( {M \cap P \cap C} \right)$
We know –
$= n\left( {M \cup P \cup C} \right) = n\left( M \right) + n\left( P \right) + n\left( C \right) - n\left( {M \cap P} \right) - n\left( {P \cap C} \right) - n\left( {C \cap M} \right) + n\left( {M \cap P \cap C} \right)$
$= 40 + 40 + 35 - 17 - 15 - 20 + 5$
$= 68$
No. of students do not fail in any subjects –
$= n\left( {M \cup P \cup C} \right) = \cup - n\left( {M \cup P \cup C} \right)$
$= 350 - 68$
$= 282$
(Total students are $350$ given)
No. of students do not fail are $282$.