Question

In a battery five dry cells each of 1.5 volt have internal resistance 0.2, 0.3, 0.4, 0.5 and 0.6$\Omega$ are present in series. The battery is connected to a $1\Omega$resistance. Identify the correct statement (s):
a) Current in the circuit will be2.5A.
b)Current in the circuit will be 1.5A
c) On short circuiting the battery 3.75A current will flow
d) Both A and B

Answer 1

In the above question five cells are connected in series to form a battery. First using Kirchhoff’s law we need to find the equivalent of the above circuit. Further using Ohm’s law we can determine the current in the circuit and select the correct alternative from those provided.
Formula used:
$V=iR$

Complete step-by-step solution:

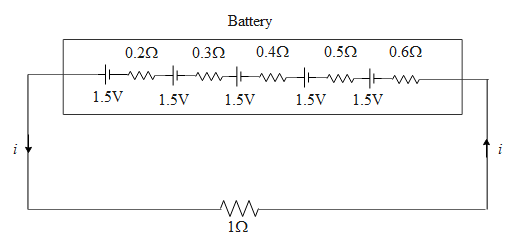
The circuit diagram above gives the brief representation of the circuit described in the question. The cells of the battery are connected in series in a similar direction. Hence using Kirchhoff's voltage law, the net emf of the battery is equal to 7.5V and net internal resistance is equal to 2 ohms.
Since the internal resistances are also in series with the external resistance ($1\Omega$), the net resistance in the above circuit is equal to $3\Omega$.
Ohm's law states that the current (i) in the circuit is directly proportional to the potential difference(V). The proportionality constant is called the resistance(R) of the circuit. The mathematical representation of this circuit is given by,
$\begin{aligned} & V=iR \\\ & \because V=7.5V,\text{ }R=3\Omega \\\ & \Rightarrow 7.5V=i\times 3\Omega \\\ & \therefore i=\dfrac{7.5V}{3\Omega }=2.5A \\\ \end{aligned}$
Therefore the correct answer of the above question is option a.

Note: The above current obtained flows across all the resistances as they all are in series. Kirchhoff’s law basically states that if we traverse along the path of current in the closed loop, then the sum of the emf that we come across is equal to the potential difference across the total resistances. In the above circuit all the individual cells of the battery are connected in series. Therefore from Kirchhoff's voltage law we got the net emf as the sum of the mf of the cells.