Question
Question: In a bangle shop, if the shopkeeper displays the bangles in the form of a square then he is left wit...
In a bangle shop, if the shopkeeper displays the bangles in the form of a square then he is left with 38 bangles with him. If he wanted to increase the size of the square by one unit each side of the square he found that 25 bangles fall short of completing the square. The actual number of bangles which he had with him in the shop was.
(a) 1690
(b) 999
(c) 538
(d) can’t be determined
Solution
Hint: For solving this question we will first understand how we can arrange a certain number of bangles in the form of a square. After that, we will assume the actual number of bangles in terms of one variable and then we will form the equations as per the given data. Then, we will solve the equations for determining the number of actual bangles which the shopkeeper had with him.
Complete step-by-step answer:
Given:
A shopkeeper had a certain number of bangles with him in the shop and he displays them in the form of a square then he is left with 38 bangles with him.
Let, the shopkeeper had N bangles actually with him.
Now, when he displays them in the form of squares then he is left with 38 bangles. Which means there are extra 38 bangles with him which are not arranged in the square.
We can understand this thing easily if we consider that he had 9 bangles with him then, he can arrange them in the form of a square with the help of the below figure:
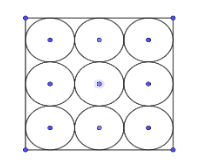
In the above figure, 9 bangles are arranged in the form of a square such that the length side of the square is of 3 units. And, if there are 16 bangles then, the length of the square will be 4 units. Now the concept here is that if there are x bangles arranged in the square then the length of the side of the square will be x units.
Now, if we arrange N bangles in form of square and 38 bangles are left then, we can say that we can arrange N−38 bangles in the form of a square in which length of the side of the square will be N−38 units.
Now, it is given to us that if we have to increase the length of the side of the square by one unit then we need more 25 bangles. Which means we can arrange N+25 bangles in the form of a square in which the length of the side of the square will be N+25 units.
Then, according to the data given in the question, we can say that the length of the side of the new square is one unit more than the length of the side of the square in which N−38 bangles were displayed. Then,
N−38+1=N+25
Squaring both sides in the above equation. Then,
[N−38+1]2=[N+25]2⇒(N−38)2+1+2×1×N−38=N+25⇒N−38+1+2N−38=N+25⇒2N−38−37=25⇒2N−38=25+37⇒2N−38=62⇒N−38=31⇒N−38=(31)2⇒N−38=961⇒N=961+38⇒N=999
Thus, the shopkeeper had 999 bangles with him.
Hence, (b) is the correct option.
Note: Here, for understanding how we can arrange bangles in the square from by visualizing the concept by considering 4 or 9 bangles and then proceed further. Then, the student must form the equations correctly and then solve them to find the correct answer. The information given in the question should be used properly to form the equations.
