Solveeit Logo
Login

Question

Question: In a \({45^ \circ } - {45^ \circ } - {90^ \circ }\) right triangle, the length of the hypotenuse is ...

In a 45∘−45∘−90∘{45^ \circ } - {45^ \circ } - {90^ \circ } right triangle, the length of the hypotenuse is 1212. How long are the legs ?

Explanation

Solution

Here, in this question we are given that two angles of the triangle are equal and the third angle is 90∘{90^ \circ }. Thus, we can say that it is an isosceles right-angled triangle whose length of hypotenuse is 1212 units. In order to solve this question, we assume the other two sides of a variable and then use Pythagoras theorem to find its value.

Complete step by step answer:
Given is a45∘−45∘−90∘{45^ \circ } - {45^ \circ } - {90^ \circ }right triangle and the length of the hypotenuse is 1212 units.According to the question, the angles of the triangle are 45∘,45∘{45^ \circ },{45^ \circ } and 90∘{90^ \circ }. Since two of the angles are the same and the third one is a right angle, so the triangle is a right-angled triangle. The length of hypotenuse is 1212 units.Let the lengths of the base and perpendicular are both xx units. Therefore, the triangle will look like-

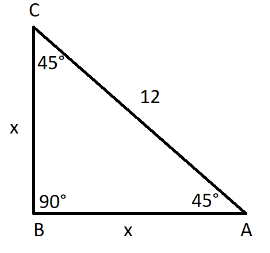
According to the Pythagoras theorem,
(hypotenuse)2=(base)2+(perpendicular)2{\left( {hypotenuse} \right)^2} = {\left( {base} \right)^2} + {\left( {perpendicular} \right)^2}
Put the values from the figure in this formula and we will get,
(12)2=(x)2+(x)2{\left( {12} \right)^2} = {\left( x \right)^2} + {\left( x \right)^2}
Now, we simplify it.
(x)2+(x)2=144 ⇒2x2=144 ⇒x2=1442 ⇒x2=72{\left( x \right)^2} + {\left( x \right)^2} = 144 \\\ \Rightarrow 2{x^2} = 144 \\\ \Rightarrow {x^2} = \dfrac{{144}}{2} \\\ \Rightarrow {x^2} = 72
Take square root on both the sides of the equation and we will get,
x2=72 ∴x=±8.5 \sqrt {{x^2}} = \sqrt {72} \\\ \therefore x = \pm 8.5 \\\
Therefore, the length of both base and perpendicular of the triangle is 8.58.5 units.

Note: The given question was easy to solve because we knew about the Pythagoras theorem. Students should avoid making calculation mistakes while finding out the sides of the triangle. Making a figure, like we did in the above question helps a lot in avoiding confusion. If the measuring unit (m, cm) is not given like in this question, so we use word units. We didn’t take the negative value because length can never be negative.