Question

In 1610, Galileo used his telescope to discover four moons around Jupiter, with mean the mean orbital radii $a$ and periods $T$:
Plot $\log a$($y$ axis) against $\log T$($x$ axis) and show that you get a straight line.

Name	$a({10^8}m)$	$T$ (days)
${I_O}$	$4.22$	$1.77$
Europa	$6.71$	$3.55$
Ganymede	$10.7$	$7.16$
Calisto	$18.8$	$16.7$

Answer 1

Take the logarithmic value of the radii and the time periods. Make a table and then plot the graph.

Complete step by step solution:
Firstly, taking the logarithmic value of radii and time periods,

Name	$\log a$	$\log T$
${I_O}$	$8.62$	$0.24$
Europa	$8.82$	$0.55$
Ganymede	$9.02$	$0.85$
Calisto	$9.27$	$1.22$

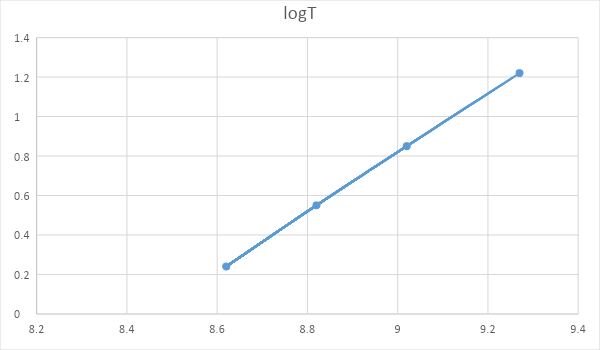
In the above given chart, we can see that the graph is a straight line.

Note: JUPITHER, IO, Europe, Ganymede and Calisto are four of Galileo's biggest stars. In December1609 or January1610, Galileo Galilei first saw them and in March1620 he was recognised as a Jupiter satellite. They became the first objects to orbit another planet than the Earth. With the exception of the Sun and the eight planets, they are one of the biggest objects in the Solar System, with radii greater than any dwarf planet. It is much larger than the planet Mercury, though just about half as large, and it's the greatest moon in the Solar system. In 4:2:1 orbital resonance, the three inner Luna’s — Io, Europa and Ganymede. While the Galilean moons are spherical, all the other moons of Jupiter are of irregular shapes owing to their poorer self-gravity.