Question

In [1, 3], the function $[x^2 + 1] + [x]$, $[x]$ denoting the greatest integer function, is continuous

• A. for all x
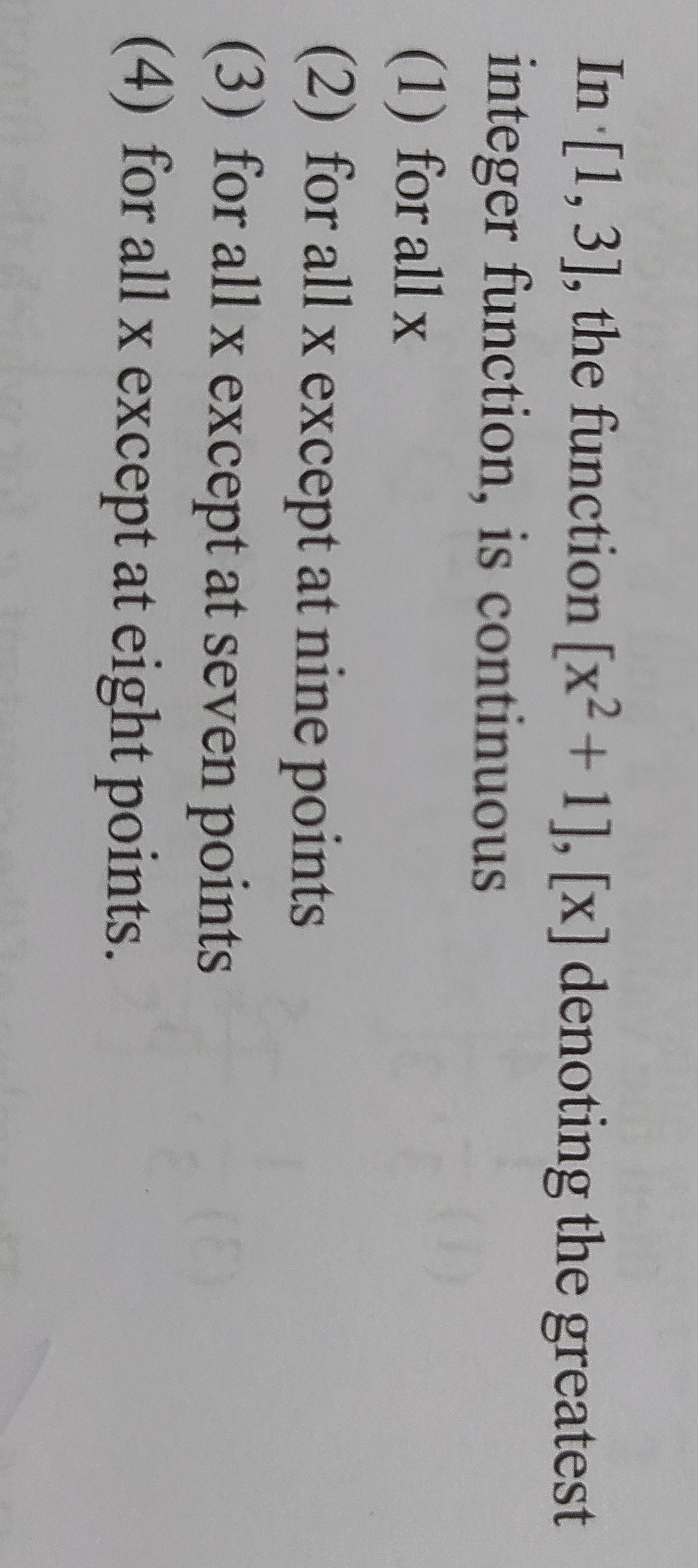
• B. for all x except at nine points
• C. for all x except at seven points
• D. for all x except at eight points.

Answer 1

Answer: (B)

for all x except at nine points

Answer 2

The function is given by $f(x) = [x^2 + 1] + [x]$, where $[y]$ denotes the greatest integer function. We need to find the points of discontinuity of $f(x)$ in the interval $[1, 3]$.

The greatest integer function $[y]$ is discontinuous when $y$ is an integer. The function $f(x)$ is a sum of two functions, $g(x) = [x^2 + 1]$ and $h(x) = [x]$. The function $f(x)$ is discontinuous at points where either $g(x)$ or $h(x)$ is discontinuous.

Consider $h(x) = [x]$. In the interval $[1, 3]$, $h(x)$ is discontinuous at integer values of $x$. The integer values in $[1, 3]$ are $1, 2, 3$.

At $x=1$, $\lim_{x \to 1^-} [x] = 0$, $\lim_{x \to 1^+} [x] = 1$. Discontinuous. At $x=2$, $\lim_{x \to 2^-} [x] = 1$, $\lim_{x \to 2^+} [x] = 2$. Discontinuous. At $x=3$, $\lim_{x \to 3^-} [x] = 2$, $\lim_{x \to 3^+} [x] = 3$. Discontinuous. So, $h(x)$ is discontinuous at $x \in \{1, 2, 3\}$ in the interval $[1, 3]$.

Consider $g(x) = [x^2 + 1]$. $g(x)$ is discontinuous when $x^2 + 1$ is an integer. Let $x^2 + 1 = k$, where $k$ is an integer. So $x^2 = k - 1$. For $x \in [1, 3]$, $x^2 \in [1^2, 3^2] = [1, 9]$. So, $x^2 + 1 \in [1+1, 9+1] = [2, 10]$. The integer values of $x^2 + 1$ in this range are $2, 3, 4, 5, 6, 7, 8, 9, 10$. The corresponding values of $x$ in $[1, 3]$ are: $x^2 + 1 = 2 \implies x^2 = 1 \implies x = 1$. $x^2 + 1 = 3 \implies x^2 = 2 \implies x = \sqrt{2}$. $x^2 + 1 = 4 \implies x^2 = 3 \implies x = \sqrt{3}$. $x^2 + 1 = 5 \implies x^2 = 4 \implies x = 2$. $x^2 + 1 = 6 \implies x^2 = 5 \implies x = \sqrt{5}$. $x^2 + 1 = 7 \implies x^2 = 6 \implies x = \sqrt{6}$. $x^2 + 1 = 8 \implies x^2 = 7 \implies x = \sqrt{7}$. $x^2 + 1 = 9 \implies x^2 = 8 \implies x = \sqrt{8} = 2\sqrt{2}$. $x^2 + 1 = 10 \implies x^2 = 9 \implies x = 3$. The values of $x$ in $[1, 3]$ where $g(x)$ is potentially discontinuous are $\{1, \sqrt{2}, \sqrt{3}, 2, \sqrt{5}, \sqrt{6}, \sqrt{7}, \sqrt{8}, 3\}$. Let $x_0$ be one of these values. As $x \to x_0^-$, $x^2+1 \to x_0^2+1 = k^-$, so $[x^2+1] \to k-1$. As $x \to x_0^+$, $x^2+1 \to x_0^2+1 = k^+$, so $[x^2+1] \to k$. Since the left and right limits are different, $g(x)$ is discontinuous at these 9 points.

The points of discontinuity of $f(x)$ are the union of the points of discontinuity of $g(x)$ and $h(x)$. Points of discontinuity for $h(x)$ in $[1, 3]$: $D_h = \{1, 2, 3\}$. Points of discontinuity for $g(x)$ in $[1, 3]$: $D_g = \{1, \sqrt{2}, \sqrt{3}, 2, \sqrt{5}, \sqrt{6}, \sqrt{7}, \sqrt{8}, 3\}$. The set of points of discontinuity for $f(x)$ in $[1, 3]$ is $D_f = D_h \cup D_g$. $D_f = \{1, 2, 3\} \cup \{1, \sqrt{2}, \sqrt{3}, 2, \sqrt{5}, \sqrt{6}, \sqrt{7}, \sqrt{8}, 3\}$. $D_f = \{1, \sqrt{2}, \sqrt{3}, 2, \sqrt{5}, \sqrt{6}, \sqrt{7}, \sqrt{8}, 3\}$. These are 9 distinct points. Let's check if the discontinuities cancel out at the common points $\{1, 2, 3\}$.

At $x=1$: $\lim_{x \to 1^-} f(x) = \lim_{x \to 1^-} [x^2 + 1] + \lim_{x \to 1^-} [x] = [2^-] + [1^-] = 1 + 0 = 1$. $\lim_{x \to 1^+} f(x) = \lim_{x \to 1^+} [x^2 + 1] + \lim_{x \to 1^+} [x] = [2^+] + [1^+] = 2 + 1 = 3$. Since the limits are different, $f(x)$ is discontinuous at $x=1$.

At $x=2$: $\lim_{x \to 2^-} f(x) = \lim_{x \to 2^-} [x^2 + 1] + \lim_{x \to 2^-} [x] = [5^-] + [2^-] = 4 + 1 = 5$. $\lim_{x \to 2^+} f(x) = \lim_{x \to 2^+} [x^2 + 1] + \lim_{x \to 2^+} [x] = [5^+] + [2^+] = 5 + 2 = 7$. Since the limits are different, $f(x)$ is discontinuous at $x=2$.

At $x=3$: We check the left limit as we are at the right endpoint of the interval $[1, 3]$. $\lim_{x \to 3^-} f(x) = \lim_{x \to 3^-} [x^2 + 1] + \lim_{x \to 3^-} [x] = [10^-] + [3^-] = 9 + 2 = 11$. $f(3) = [3^2 + 1] + [3] = [10] + [3] = 10 + 3 = 13$. Since the left limit is not equal to the function value, $f(x)$ is discontinuous at $x=3$.

For the points in $D_g$ that are not in $D_h$, i.e., $\{\sqrt{2}, \sqrt{3}, \sqrt{5}, \sqrt{6}, \sqrt{7}, \sqrt{8}\}$, $g(x)$ is discontinuous and $h(x)$ is continuous. The sum of a discontinuous function and a continuous function is discontinuous. So $f(x)$ is discontinuous at these 6 points.

The set of points of discontinuity for $f(x)$ in $[1, 3]$ is $\{1, \sqrt{2}, \sqrt{3}, 2, \sqrt{5}, \sqrt{6}, \sqrt{7}, \sqrt{8}, 3\}$. These are 9 distinct points. The function is continuous for all $x$ in $[1, 3]$ except at these 9 points.