Question

Evaluate $\int \frac{1-x^2}{1+x^2}dx$.

Answer 1

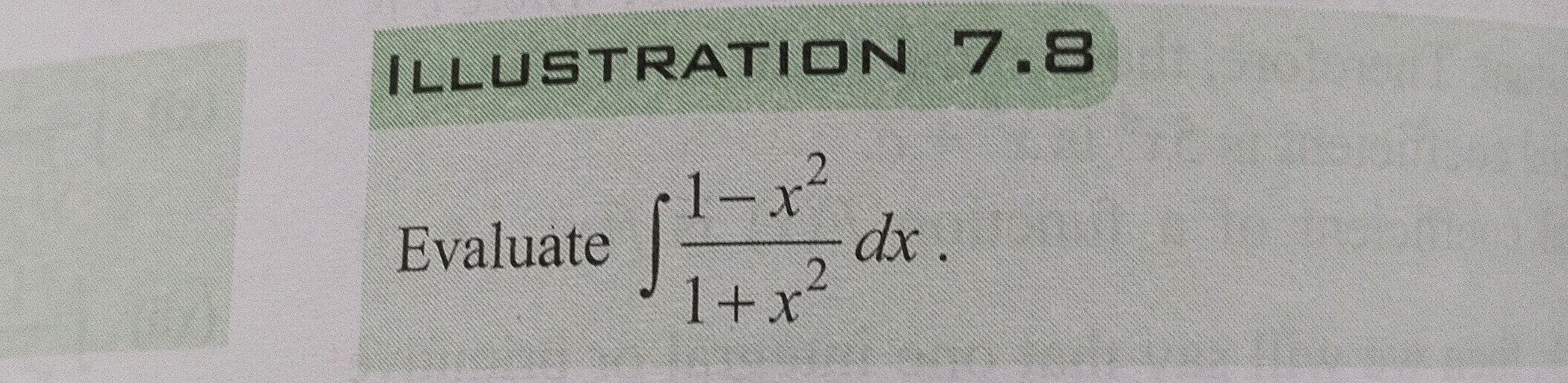
$-x + 2\tan^{-1}(x) + C$

Answer 2

To evaluate the integral $\int \frac{1-x^2}{1+x^2}dx$, we observe that the degree of the numerator is equal to the degree of the denominator. In such cases, we can simplify the integrand by performing polynomial long division or by algebraically manipulating the numerator.

We can rewrite the numerator $1-x^2$ by adding and subtracting $1$ in a strategic way to match the denominator $1+x^2$:

$1-x^2 = -(x^2-1) = -(x^2+1-2) = -(x^2+1) + 2$

Now, substitute this back into the integral:

$\int \frac{-(x^2+1) + 2}{1+x^2}dx$

Split the fraction into two separate terms:

$= \int \left( \frac{-(x^2+1)}{1+x^2} + \frac{2}{1+x^2} \right) dx$

Simplify the first term:

$= \int \left( -1 + \frac{2}{1+x^2} \right) dx$

Now, integrate each term separately:

$= \int -1 dx + \int \frac{2}{1+x^2} dx$

$= -x + 2 \int \frac{1}{1+x^2} dx$

We know the standard integral formula $\int \frac{1}{1+x^2} dx = \tan^{-1}(x) + C$.

Applying this formula, we get:

$= -x + 2\tan^{-1}(x) + C$

where $C$ is the constant of integration.