Question

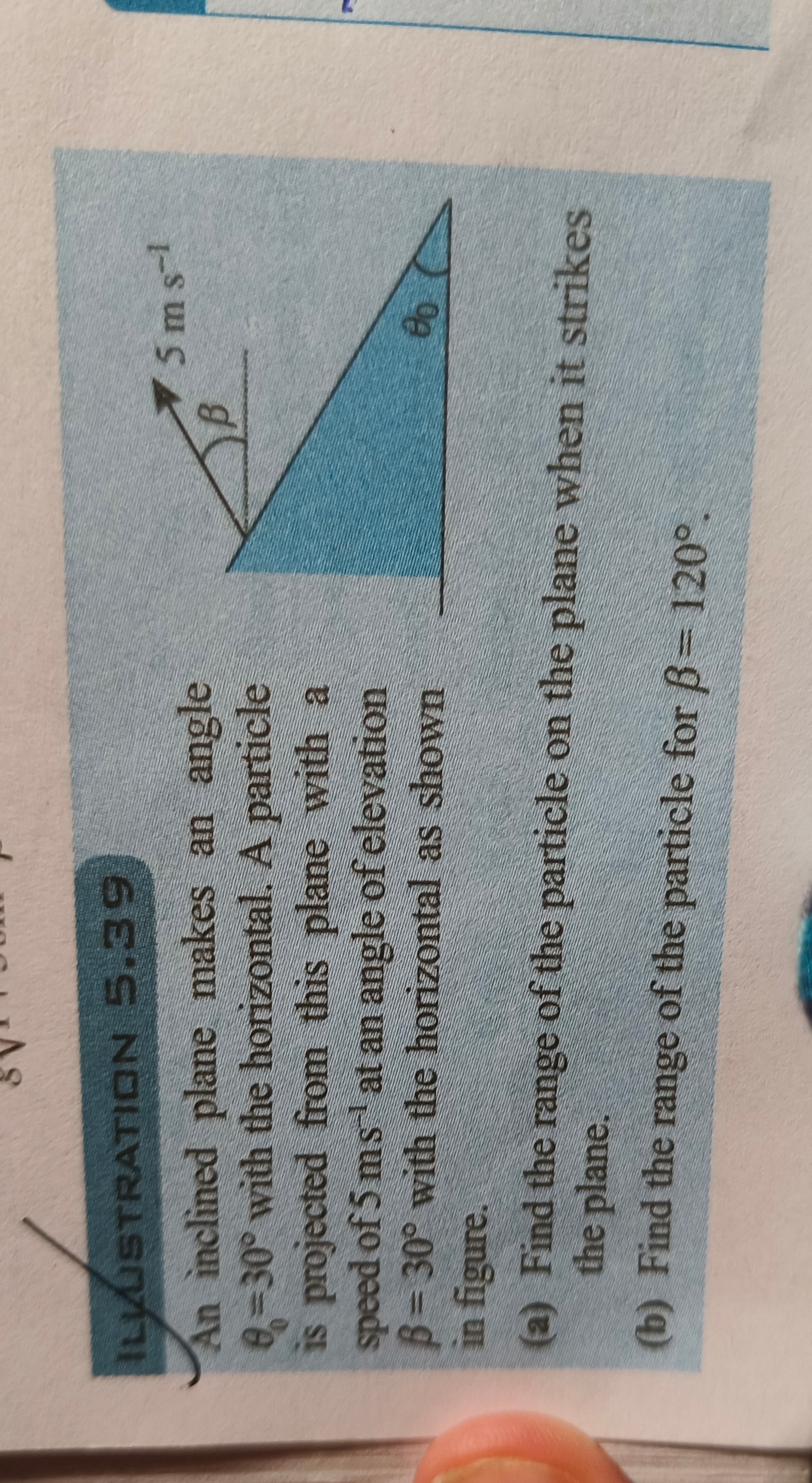
An inclined plane makes an angle $\theta_0$=30° with the horizontal. A particle is projected from this plane with a speed of 5 ms⁻¹ at an angle of elevation $\beta$ = 30° with the horizontal as shown in figure.

Answer 1

a) 5/3 m, b) 10/3 m

Answer 2

The problem involves projectile motion on an inclined plane. We will use a coordinate system where the x-axis is along the inclined plane (upwards) and the y-axis is perpendicular to the inclined plane (upwards).

Given:

• Angle of inclination of the plane with the horizontal, $\theta_0 = 30^\circ$.
• Initial speed of projection, $u = 5 \text{ ms}^{-1}$.
• Acceleration due to gravity, $g = 10 \text{ ms}^{-2}$ (standard assumption if not specified).

Interpretation of Projection Angle: The problem states "angle of elevation $\beta$ = 30° with the horizontal as shown in figure." and for part (a), $\beta = 30^\circ$. If $\beta$ is the angle with the horizontal, and $\theta_0$ is the angle of the plane with the horizontal, then $\beta = \theta_0$ implies the projectile is launched parallel to the inclined plane. In such a scenario, the particle would not leave the plane and then "strike the plane" as projectile motion. This is a common ambiguity in such problems. Considering similar problems (like the one provided), it's often implied that the given projection angle is with respect to the inclined plane itself, especially when the problem asks for the range on the plane. Let's assume that $\beta$ is the angle of projection with respect to the inclined plane. Let's denote this angle as $\alpha$. So, $\alpha$ is the angle of projection with respect to the inclined plane. The angle of the initial velocity vector with the horizontal would then be $\beta_{actual} = \alpha + \theta_0$.

Formulas for Projectile Motion on an Inclined Plane (projected up the incline): Let $\alpha$ be the angle of projection with respect to the inclined plane. The time of flight $T$ is given by: $T = \frac{2u \sin \alpha}{g \cos \theta_0}$ The range $R$ on the inclined plane is given by: $R = \frac{2u^2 \sin \alpha \cos(\alpha + \theta_0)}{g \cos^2 \theta_0}$

Part (a): Find the range of the particle on the plane when it strikes the plane for $\beta = 30^\circ$. Assuming $\beta$ here means $\alpha$, the angle of projection with respect to the inclined plane. So, $\alpha = 30^\circ$. $\theta_0 = 30^\circ$. $u = 5 \text{ ms}^{-1}$.

Substitute these values into the range formula: $R = \frac{2(5^2) \sin(30^\circ) \cos(30^\circ + 30^\circ)}{10 \cos^2(30^\circ)}$ $R = \frac{2 \times 25 \times \sin(30^\circ) \cos(60^\circ)}{10 \times (\cos(30^\circ))^2}$ We know: $\sin(30^\circ) = \frac{1}{2}$, $\cos(30^\circ) = \frac{\sqrt{3}}{2}$, $\cos(60^\circ) = \frac{1}{2}$.

$R = \frac{50 \times \frac{1}{2} \times \frac{1}{2}}{10 \times \left(\frac{\sqrt{3}}{2}\right)^2}$ $R = \frac{50 \times \frac{1}{4}}{10 \times \frac{3}{4}}$ $R = \frac{12.5}{7.5}$ $R = \frac{125}{75} = \frac{5 \times 25}{3 \times 25} = \frac{5}{3} \text{ m}$

Part (b): Find the range of the particle for $\beta = 120^\circ$. Here, $\beta = 120^\circ$ is given as the angle of elevation with the horizontal. Since the plane is inclined at $\theta_0 = 30^\circ$, the angle of projection with respect to the inclined plane is $\alpha = \beta - \theta_0$. $\alpha = 120^\circ - 30^\circ = 90^\circ$. This means the particle is projected vertically upwards, perpendicular to the inclined plane.

Substitute these values into the range formula: $R = \frac{2u^2 \sin \alpha \cos(\alpha + \theta_0)}{g \cos^2 \theta_0}$ $R = \frac{2(5^2) \sin(90^\circ) \cos(90^\circ + 30^\circ)}{10 \cos^2(30^\circ)}$ $R = \frac{2 \times 25 \times \sin(90^\circ) \cos(120^\circ)}{10 \times (\cos(30^\circ))^2}$ We know: $\sin(90^\circ) = 1$, $\cos(120^\circ) = -\frac{1}{2}$, $\cos(30^\circ) = \frac{\sqrt{3}}{2}$.

$R = \frac{50 \times 1 \times \left(-\frac{1}{2}\right)}{10 \times \left(\frac{\sqrt{3}}{2}\right)^2}$ $R = \frac{-25}{10 \times \frac{3}{4}}$ $R = \frac{-25}{7.5}$ $R = \frac{-250}{75} = \frac{-10 \times 25}{3 \times 25} = -\frac{10}{3} \text{ m}$

A negative range indicates that the particle lands behind the point of projection (down the incline from the projection point). This is physically possible if the projection is such that the particle goes high enough and then falls back down, passing the projection point and landing on the plane below it.

The question usually implies magnitude of range. So, the magnitude of range is $10/3 \text{ m}$.