Question

Evaluate $\lim_{x\to \frac{3\pi}{4}} \frac{1+\sqrt[3]{\tan x}}{1-2\cos^2 x}$.

Answer 1

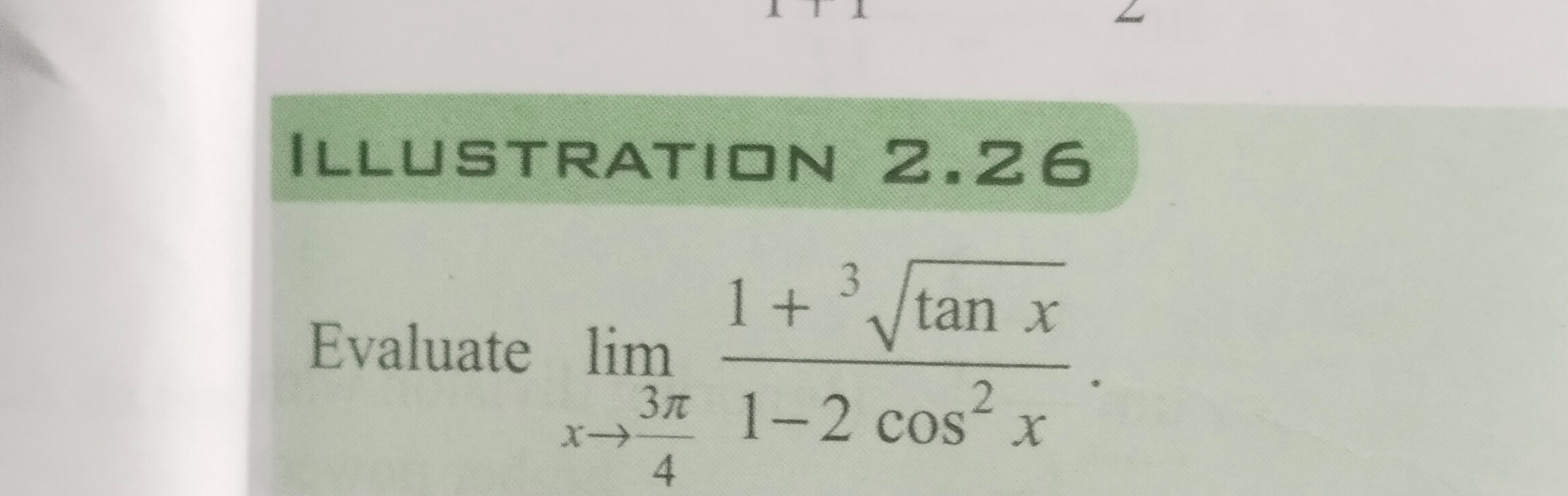
The limit is -1/3

Answer 2

The problem asks us to evaluate the limit: $\lim_{x\to \frac{3\pi}{4}} \frac{1+\sqrt[3]{\tan x}}{1-2\cos^2 x}$

Step 1: Check for indeterminate form. Substitute $x = \frac{3\pi}{4}$ into the expression: Numerator: $1+\sqrt[3]{\tan(\frac{3\pi}{4})} = 1+\sqrt[3]{-1} = 1-1 = 0$. Denominator: $1-2\cos^2(\frac{3\pi}{4})$. We know $\cos(\frac{3\pi}{4}) = -\frac{1}{\sqrt{2}}$. So, $1-2\left(-\frac{1}{\sqrt{2}}\right)^2 = 1-2\left(\frac{1}{2}\right) = 1-1 = 0$. Since the limit is of the $\frac{0}{0}$ indeterminate form, we can apply L'Hopital's Rule.

Step 2: Apply L'Hopital's Rule. Let $f(x) = 1+\sqrt[3]{\tan x}$ and $g(x) = 1-2\cos^2 x$. L'Hopital's Rule states that if $\lim_{x\to c} \frac{f(x)}{g(x)}$ is of the form $\frac{0}{0}$ or $\frac{\infty}{\infty}$, then $\lim_{x\to c} \frac{f(x)}{g(x)} = \lim_{x\to c} \frac{f'(x)}{g'(x)}$, provided the latter limit exists.

Step 3: Calculate the derivatives of the numerator and the denominator. For the numerator, $f(x) = 1+(\tan x)^{1/3}$: $f'(x) = \frac{d}{dx}(1+(\tan x)^{1/3}) = 0 + \frac{1}{3}(\tan x)^{\frac{1}{3}-1} \cdot \frac{d}{dx}(\tan x)$ $f'(x) = \frac{1}{3}(\tan x)^{-2/3} \cdot \sec^2 x = \frac{\sec^2 x}{3(\tan x)^{2/3}}$

For the denominator, $g(x) = 1-2\cos^2 x$: $g'(x) = \frac{d}{dx}(1-2\cos^2 x) = 0 - 2 \cdot (2\cos x \cdot (-\sin x))$ $g'(x) = 4\sin x \cos x$ Using the double angle identity $\sin(2x) = 2\sin x \cos x$, we can simplify $g'(x)$: $g'(x) = 2(2\sin x \cos x) = 2\sin(2x)$

Step 4: Evaluate the derivatives at $x = \frac{3\pi}{4}$. For $f'(\frac{3\pi}{4})$: We know $\tan(\frac{3\pi}{4}) = -1$ and $\cos(\frac{3\pi}{4}) = -\frac{1}{\sqrt{2}}$, so $\sec(\frac{3\pi}{4}) = \frac{1}{\cos(\frac{3\pi}{4})} = -\sqrt{2}$. $f'(\frac{3\pi}{4}) = \frac{(-\sqrt{2})^2}{3(-1)^{2/3}} = \frac{2}{3 \cdot ((-1)^2)^{1/3}} = \frac{2}{3 \cdot (1)^{1/3}} = \frac{2}{3 \cdot 1} = \frac{2}{3}$

For $g'(\frac{3\pi}{4})$: $g'(\frac{3\pi}{4}) = 2\sin\left(2 \cdot \frac{3\pi}{4}\right) = 2\sin\left(\frac{3\pi}{2}\right)$ We know $\sin(\frac{3\pi}{2}) = -1$. $g'(\frac{3\pi}{4}) = 2(-1) = -2$

Step 5: Compute the limit. $\lim_{x\to \frac{3\pi}{4}} \frac{1+\sqrt[3]{\tan x}}{1-2\cos^2 x} = \frac{f'(\frac{3\pi}{4})}{g'(\frac{3\pi}{4})} = \frac{2/3}{-2} = \frac{2}{3 \cdot (-2)} = -\frac{1}{3}$

The final answer is $-\frac{1}{3}$.

Explanation of the solution: The limit is of the $\frac{0}{0}$ indeterminate form. L'Hopital's Rule is applied. The derivatives of the numerator ($1+\sqrt[3]{\tan x}$) and the denominator ($1-2\cos^2 x$) are calculated as $\frac{\sec^2 x}{3(\tan x)^{2/3}}$ and $2\sin(2x)$ respectively. Evaluating these derivatives at $x=\frac{3\pi}{4}$ yields $\frac{2}{3}$ for the numerator's derivative and $-2$ for the denominator's derivative. The ratio of these values gives the limit, which is $-\frac{1}{3}$.