Question
Question: Evaluate $\lim_{x\to 1}\frac{x^2+x\log_e x-\log_ex-1}{(x^2-1)}.$...
Evaluate limx→1(x2−1)x2+xlogex−logex−1.
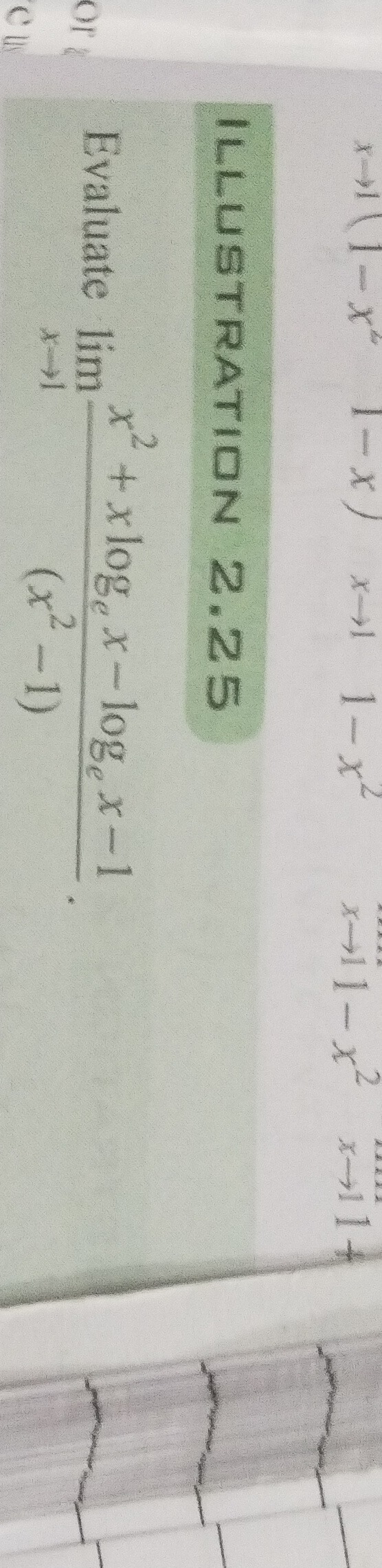
1
Solution
The given limit is: limx→1(x2−1)x2+xlogex−logex−1
First, substitute x=1 into the expression to determine its form:
Numerator: 12+1⋅loge1−loge1−1=1+1⋅0−0−1=0
Denominator: 12−1=0
Since the limit is in the 00 indeterminate form, we can use either L'Hopital's Rule or algebraic manipulation.
Method 1: Using L'Hopital's Rule
Let f(x)=x2+xlogex−logex−1 and g(x)=x2−1. We need to find the derivatives of f(x) and g(x) with respect to x.
Derivative of the numerator f′(x): f′(x)=dxd(x2+xlogex−logex−1) Using the product rule for xlogex: dxd(uv)=u′v+uv′. Here u=x,v=logex, so u′=1,v′=x1. f′(x)=2x+(1⋅logex+x⋅x1)−x1−0 f′(x)=2x+logex+1−x1
Derivative of the denominator g′(x): g′(x)=dxd(x2−1) g′(x)=2x
Now, apply L'Hopital's Rule: limx→1g′(x)f′(x)=limx→12x2x+logex+1−x1 Substitute x=1: 2(1)2(1)+loge1+1−11=22+0+1−1=22=1
Method 2: Algebraic Manipulation
Factorize the numerator and the denominator.
Numerator: x2+xlogex−logex−1
Group terms: (x2−1)+(xlogex−logex)
Factor out common terms: (x−1)(x+1)+logex(x−1)
Factor out (x−1): (x−1)[(x+1)+logex]
Denominator: x2−1
Factorize: (x−1)(x+1)
Now, substitute these back into the limit expression: limx→1(x−1)(x+1)(x−1)[(x+1)+logex] Since x→1, x=1, so we can cancel the common term (x−1): limx→1(x+1)(x+1)+logex Substitute x=1: (1+1)(1+1)+loge1=22+0=22=1
Both methods yield the same result.
Explanation of the solution:
The limit is in the 00 indeterminate form.
Method 1 (L'Hopital's Rule): Differentiate the numerator and denominator separately. f′(x)=2x+logex+1−x1 and g′(x)=2x. Substitute x=1 into g′(x)f′(x) to get 22+0+1−1=22=1.
Method 2 (Algebraic Manipulation): Factor the numerator as (x−1)(x+1)+logex(x−1)=(x−1)[(x+1)+logex]. Factor the denominator as (x−1)(x+1). Cancel the common (x−1) term and substitute x=1 into the simplified expression (x+1)(x+1)+logex to get 1+11+1+0=22=1.
The limit evaluates to 1.
