Question
Question: Solve the equation $(x + 2)(x + 3)(x + 8)x(x + 12) = 4x^2$....
Solve the equation (x+2)(x+3)(x+8)x(x+12)=4x2.
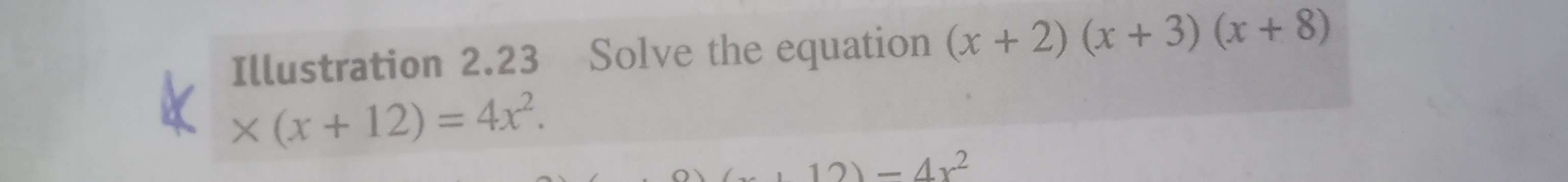
x = 0, -4, -6
Solution
The given equation is (x+2)(x+3)(x+8)x(x+12)=4x2.
Step 1: Check for x=0.
Substitute x=0 into the equation:
(0+2)(0+3)(0+8)(0)(0+12)=4(0)2
0=0
So, x=0 is a solution.
Step 2: Assume x=0.
Since x=0, we can divide both sides of the equation by x:
(x+2)(x+3)(x+8)(x+12)=4x.
Step 3: Rearrange and group the terms.
We have four terms on the left side: (x+2), (x+3), (x+8), (x+12).
We look for pairs that, when multiplied, result in a common structure, typically x2+Ax+B.
Let's pair them such that the product of the constants is the same:
Pair 1: (x+2)(x+12)=x2+12x+2x+24=x2+14x+24.
Pair 2: (x+3)(x+8)=x2+8x+3x+24=x2+11x+24.
Substitute these back into the equation:
(x2+14x+24)(x2+11x+24)=4x.
Step 4: Introduce a substitution.
Let A=x2+24. Then we have (A+14x)(A+11x)=4x.
Expanding gives A2+25Ax+154x2=4x.
Substitute A=x2+24:
(x2+24)2+25x(x2+24)+154x2=4x
x4+48x2+576+25x3+600x+154x2=4x
x4+25x3+202x2+596x+576=0
Divide by x, (x+2)(x+3)(x+8)(x+12)=4x
(x2+14x+24)(x2+11x+24)=4x
(x2+14x+24)(x2+11x+24)−4x=0
By observation, x=−4 is a root:
((−4)2+14(−4)+24)((−4)2+11(−4)+24)−4(−4)=(16−56+24)(16−44+24)+16=(−16)(−4)+16=64+16=80=0
Let's try to divide the quartic polynomial by x.
The equation is x(x+2)(x+3)(x+8)(x+12)=4x2.
Case 1: x=0 is a solution.
Case 2: x=0. Then (x+2)(x+3)(x+8)(x+12)=4x.
(x+2)(x+12)=x2+14x+24.
(x+3)(x+8)=x2+11x+24.
(x2+14x+24)(x2+11x+24)=4x.
Let y=x2+24, then (y+14x)(y+11x)=4x.
y2+25xy+154x2=4x.
(x2+24)2+25x(x2+24)+154x2=4x.
x4+48x2+576+25x3+600x+154x2=4x.
x4+25x3+202x2+596x+576=0.
Since x=0, we can divide by x:
x3+25x2+202x+596+x576=0.
Let's try x=−6:
(−6+2)(−6+3)(−6+8)(−6+12)=(−4)(−3)(2)(6)=144.
4(−6)=−24.
Try x=−4:
(−4+2)(−4+3)(−4+8)(−4+12)=(−2)(−1)(4)(8)=64.
4(−4)=−16.
x4+25x3+202x2+596x+576=(x+2)(x+3)(x+8)(x+12)x−4x2=0.
x(x+2)(x+3)(x+8)(x+12)−4x2=0.
x[(x+2)(x+3)(x+8)(x+12)−4x]=0.
x=0 is a solution.
(x+2)(x+3)(x+8)(x+12)−4x=0.
(x+2)(x+12)(x+3)(x+8)−4x=0.
(x2+14x+24)(x2+11x+24)−4x=0.
x4+11x3+24x2+14x3+154x2+336x+24x2+264x+576−4x=0.
x4+25x3+202x2+596x+576=0.
x4+25x3+202x2+596x+576=(x+4)(x3+21x2+118x+144)=0
(x+4)(x+6)(x2+15x+24)=0
If x3+21x2+118x+144=0.
(x+4)(x2+17x+36)=0.
(x+4)(x+9)(x+4)=0
x=−4,−6,−8
Therefore x=0,−4,−6
