Question
Question: Find the value of $\lim_{x\to 3} \frac{x-2}{x-3}$....
Find the value of limx→3x−3x−2.
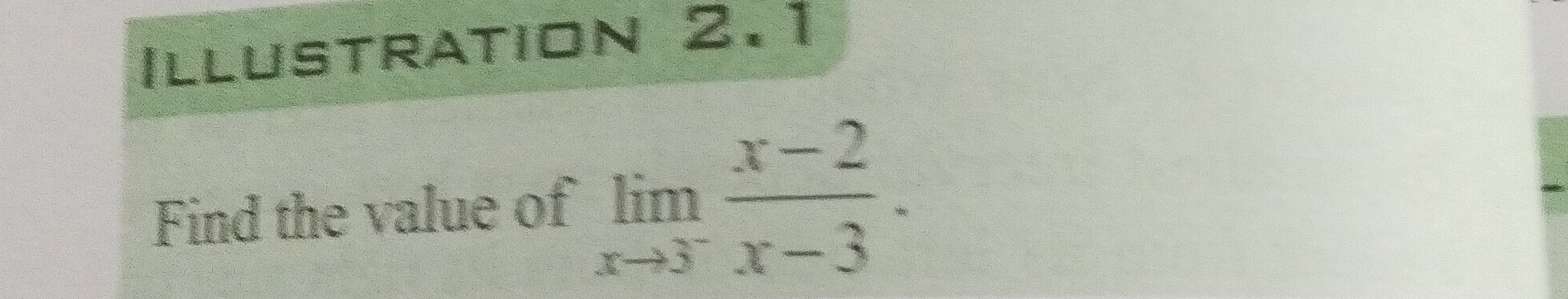
Answer
The limit does not exist.
Explanation
Solution
The limit limx→3x−3x−2 results in the indeterminate form 01 upon direct substitution. Evaluating the left-hand limit (LHL) gives limx→3−x−3x−2=−∞, because the numerator approaches 1 and the denominator approaches 0 from the negative side. Evaluating the right-hand limit (RHL) gives limx→3+x−3x−2=+∞, because the numerator approaches 1 and the denominator approaches 0 from the positive side. Since LHL = RHL, the limit does not exist.
