Question

Find the value of $\lim_{x \to 3} \frac{x-2}{x-3}$.

Answer 1

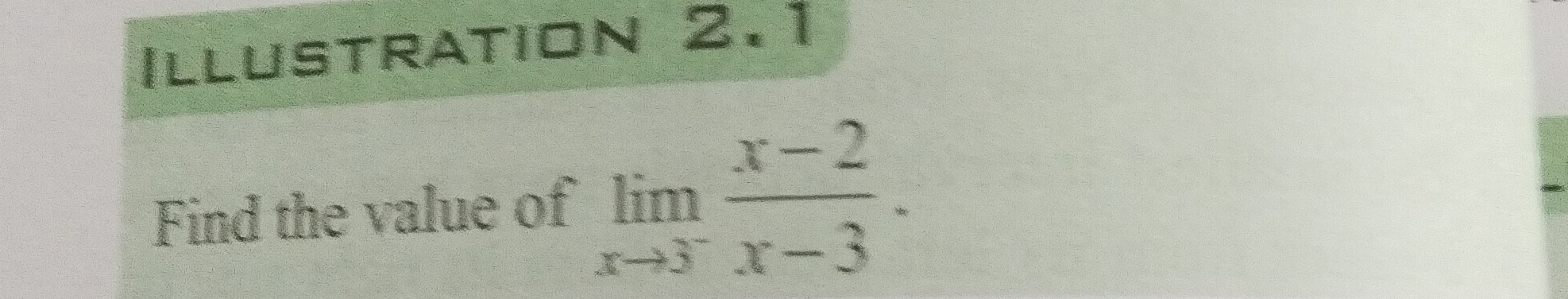
Does not exist

Answer 2

To find the value of $\lim_{x \to 3} \frac{x-2}{x-3}$, we first attempt direct substitution of $x=3$ into the expression.

Numerator: $3-2 = 1$ Denominator: $3-3 = 0$

Since the denominator approaches zero and the numerator approaches a non-zero constant (1), the limit will be either $+\infty$, $-\infty$, or it will not exist. To determine this, we need to evaluate the left-hand limit (LHL) and the right-hand limit (RHL).

1. Right-Hand Limit (RHL): $\lim_{x \to 3^+} \frac{x-2}{x-3}$

As $x$ approaches 3 from the right side (i.e., $x$ is slightly greater than 3), let $x = 3+h$, where $h \to 0^+$.

Substitute $x = 3+h$ into the expression: $\frac{(3+h)-2}{(3+h)-3} = \frac{1+h}{h}$

As $h \to 0^+$, the numerator $(1+h)$ approaches $1$ (a positive number).

As $h \to 0^+$, the denominator $h$ approaches $0$ from the positive side (a very small positive number).

Therefore, $\lim_{h \to 0^+} \frac{1+h}{h} = \frac{1}{\text{small positive number}} = +\infty$.

2. Left-Hand Limit (LHL): $\lim_{x \to 3^-} \frac{x-2}{x-3}$

As $x$ approaches 3 from the left side (i.e., $x$ is slightly less than 3), let $x = 3-h$, where $h \to 0^+$.

Substitute $x = 3-h$ into the expression: $\frac{(3-h)-2}{(3-h)-3} = \frac{1-h}{-h}$

As $h \to 0^+$, the numerator $(1-h)$ approaches $1$ (a positive number).

As $h \to 0^+$, the denominator $-h$ approaches $0$ from the negative side (a very small negative number).

Therefore, $\lim_{h \to 0^+} \frac{1-h}{-h} = \frac{1}{\text{small negative number}} = -\infty$.

Conclusion: Since the right-hand limit ($+\infty$) and the left-hand limit ($-\infty$) are not equal, the limit $\lim_{x \to 3} \frac{x-2}{x-3}$ does not exist.