Question

Solve $\frac{d^2y}{dx^2} = (\frac{dy}{dx})^2$

Answer 1

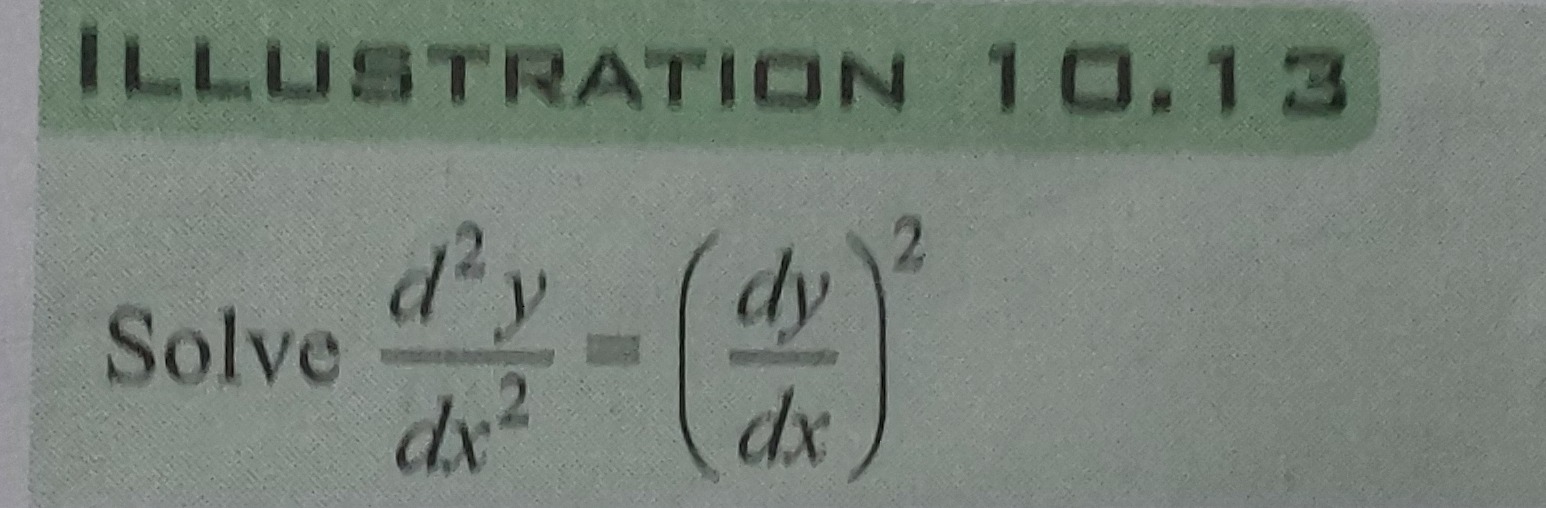
The general solution is $y = -\ln|x + C_1| + C_2$.

The singular solution is $y = C$.

Answer 2

The given differential equation is: $\frac{d^2y}{dx^2} = \left(\frac{dy}{dx}\right)^2$

This is a second-order ordinary differential equation. We can reduce its order by a suitable substitution.

Step 1: Reduce the order of the differential equation.

Let $p = \frac{dy}{dx}$.
Then, the second derivative $\frac{d^2y}{dx^2}$ can be expressed as $\frac{dp}{dx}$.
Substituting these into the given equation, we get: $\frac{dp}{dx} = p^2$ This is a first-order differential equation in terms of $p$ and $x$.

Step 2: Solve the first-order differential equation for $p$.

This is a separable differential equation.

Case 1: $p \neq 0$

Separate the variables: $\frac{dp}{p^2} = dx$ Integrate both sides: $\int p^{-2} dp = \int dx$ $-\frac{1}{p} = x + C_1$ where $C_1$ is the first constant of integration.

Now, solve for $p$: $p = -\frac{1}{x + C_1}$

Step 3: Substitute back $p = \frac{dy}{dx}$ and solve for $y$.

We have $p = \frac{dy}{dx}$, so: $\frac{dy}{dx} = -\frac{1}{x + C_1}$ This is another first-order separable differential equation.
Separate the variables: $dy = -\frac{1}{x + C_1} dx$ Integrate both sides: $\int dy = \int -\frac{1}{x + C_1} dx$ $y = -\ln|x + C_1| + C_2$ where $C_2$ is the second constant of integration.
This is the general solution for the case where $p \neq 0$.

Case 2: $p = 0$

If $p = \frac{dy}{dx} = 0$, then $\frac{d^2y}{dx^2} = 0$.
Substitute these into the original differential equation: $0 = (0)^2$ $0 = 0$ This is true, so $p=0$ is a valid solution for $\frac{dp}{dx} = p^2$.
If $\frac{dy}{dx} = 0$, then integrating with respect to $x$ gives: $y = C$ where $C$ is an arbitrary constant. This is a singular solution, as it cannot be obtained from the general solution $y = -\ln|x + C_1| + C_2$ for any choice of $C_1$ and $C_2$.

Summary of Solutions:

The general solution is $y = -\ln|x + C_1| + C_2$.
A singular solution is $y = C$.

The solution can also be written as $y + \ln|x + C_1| = C_2$.

Explanation of the solution:

The second-order differential equation is reduced to a first-order separable equation by substituting $p = dy/dx$. This first-order equation is then solved for $p$. The expression for $p$ is then substituted back as $dy/dx$, leading to another first-order separable equation which is solved to find $y$. A special case where $dy/dx = 0$ is also checked, leading to a singular solution.