Question

Solve for x: $x + \log_{10}(2^x + 1) = \log_{10} 6 + x \log_{10} 5$

Answer 1

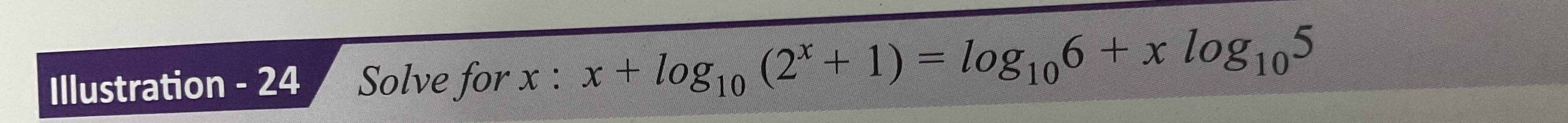
The solution for the equation is $x=1$.

Answer 2

The given equation is $x + \log_{10}(2^x + 1) = \log_{10} 6 + x \log_{10} 5$.

Rearrange the terms to group terms involving $x$: $x - x \log_{10} 5 + \log_{10}(2^x + 1) = \log_{10} 6$

Factor out $x$ from the first two terms: $x(1 - \log_{10} 5) + \log_{10}(2^x + 1) = \log_{10} 6$

Use the property $1 = \log_{10} 10$: $x(\log_{10} 10 - \log_{10} 5) + \log_{10}(2^x + 1) = \log_{10} 6$

Use the property $\log_b A - \log_b B = \log_b (A/B)$: $x \log_{10} (10/5) + \log_{10}(2^x + 1) = \log_{10} 6$

Simplify: $x \log_{10} 2 + \log_{10}(2^x + 1) = \log_{10} 6$

Use the property $a \log_b c = \log_b c^a$: $\log_{10} 2^x + \log_{10}(2^x + 1) = \log_{10} 6$

Use the property $\log_b A + \log_b B = \log_b (A \times B)$: $\log_{10} [2^x (2^x + 1)] = \log_{10} 6$

Since the logarithms are equal and have the same base, their arguments must be equal: $2^x (2^x + 1) = 6$

Let $y = 2^x$. Since $2^x > 0$ for all real $x$, $y > 0$. The equation becomes a quadratic equation in terms of $y$: $y(y + 1) = 6$ $y^2 + y - 6 = 0$

Factor the quadratic equation: $(y + 3)(y - 2) = 0$

This gives two possible solutions for $y$: $y + 3 = 0 \implies y = -3$ $y - 2 = 0 \implies y = 2$

Substitute back $y = 2^x$: Case 1: $2^x = -3$. This equation has no real solution because the exponential function $2^x$ is always positive for real values of $x$. Case 2: $2^x = 2$. This can be written as $2^x = 2^1$. Equating the exponents, we get $x = 1$.

We should verify the solution $x=1$ in the original equation. Left Hand Side (LHS): $1 + \log_{10}(2^1 + 1) = 1 + \log_{10}(2 + 1) = 1 + \log_{10} 3$. Using the property $1 = \log_{10} 10$, LHS $= \log_{10} 10 + \log_{10} 3 = \log_{10} (10 \times 3) = \log_{10} 30$.

Right Hand Side (RHS): $\log_{10} 6 + 1 \times \log_{10} 5 = \log_{10} 6 + \log_{10} 5$. Using the property $\log_b A + \log_b B = \log_b (A \times B)$, RHS $= \log_{10} (6 \times 5) = \log_{10} 30$.

Since LHS = RHS, the solution $x = 1$ is correct.