Question
Question: If $log_{10}5 = a$ and $log_{10}3 = b$ then :...
If log105=a and log103=b then :
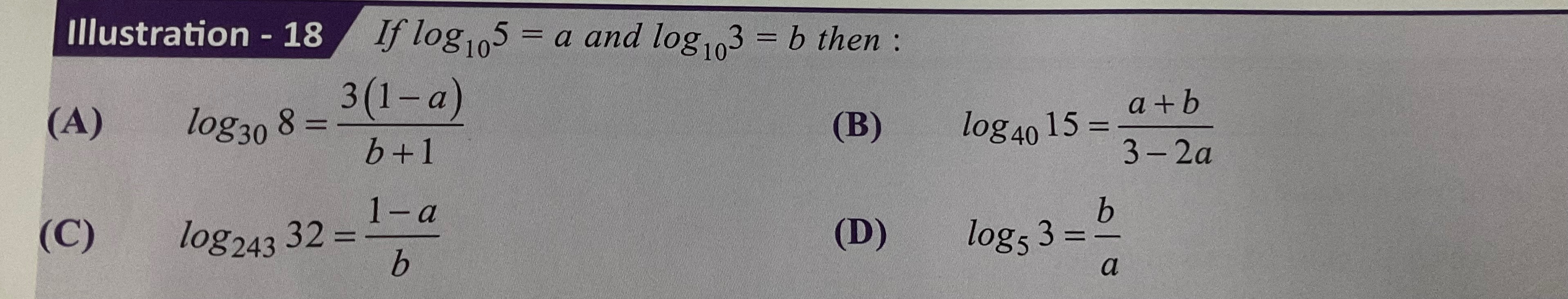
log308=b+13(1−a)
log4015=3−2aa+b
log24332=b1−a
log53=ab
(A), (B), (C), (D)
Solution
Given log105=a and log103=b.
We know that log1010=1.
Using the property logb(xy)=logbx+logby, we have log1010=log10(5×2)=log105+log102.
So, 1=a+log102, which gives log102=1−a.
Now, we evaluate each option using the change of base formula logcx=logdclogdx with d=10.
(A) log308: log308=log1030log108=log10(3×10)log10(23)=log103+log10103log102=b+13(1−a). Option (A) is correct.
(B) log4015: log4015=log1040log1015=log10(4×10)log10(3×5)=log10(22×10)log103+log105=log10(22)+log1010log103+log105=2log102+1b+a.
Substitute log102=1−a: 2(1−a)+1a+b=2−2a+1a+b=3−2aa+b. Option (B) is correct.
(C) log24332: log24332=log10243log1032=log10(35)log10(25)=5log1035log102=log103log102.
Substitute log102=1−a and log103=b: b1−a. Option (C) is correct.
(D) log53: log53=log105log103=ab. Option (D) is correct.
All four options are correct.
