Question

$I=\int_{\frac{-1}{\sqrt{3}}}^{\frac{1}{\sqrt{3}}} \frac{(cosx-sinx)dx}{1+2sin2x}$

Answer 1

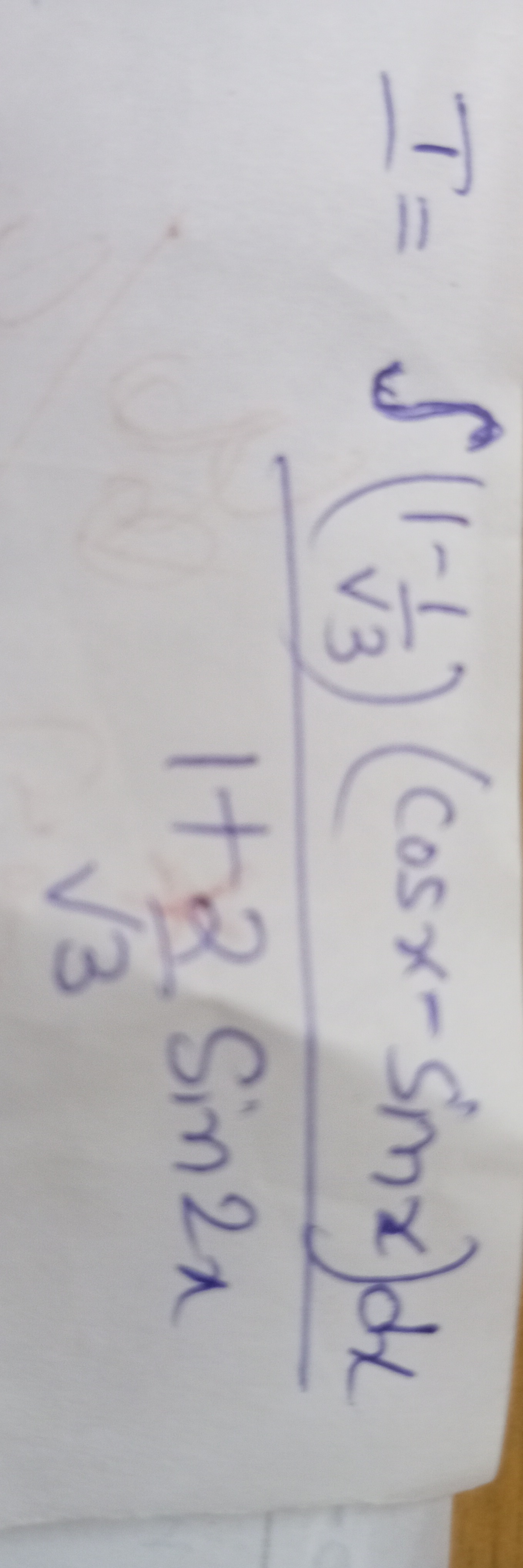
Diverges

Answer 2

To evaluate the integral $I=\int_{\frac{-1}{\sqrt{3}}}^{\frac{1}{\sqrt{3}}} \frac{(cosx-sinx)dx}{1+2sin2x}$, we must consider the possibility of singularities within the interval of integration.

First, we identify potential singularities by finding where the denominator is zero: $1 + 2\sin(2x) = 0$ $\sin(2x) = -\frac{1}{2}$

The general solution for $2x$ is: $2x = -\frac{\pi}{6} + 2n\pi \quad \text{or} \quad 2x = \frac{7\pi}{6} + 2n\pi$ Where $n$ is an integer. Thus, $x = -\frac{\pi}{12} + n\pi \quad \text{or} \quad x = \frac{7\pi}{12} + n\pi$

We need to determine if any of these singularities lie within the interval $[-\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}]$. Since $\frac{1}{\sqrt{3}} \approx 0.577$ and $\frac{\pi}{12} \approx 0.262$, we can see that $x = -\frac{\pi}{12}$ is within the interval of integration.

Specifically, $-\frac{1}{\sqrt{3}} \le -\frac{\pi}{12} \le \frac{1}{\sqrt{3}}$ because $-0.577 \le -0.262 \le 0.577$.

Since there is a singularity at $x = -\frac{\pi}{12}$ within the interval of integration, the integral is improper. The behavior of the integrand near this singularity determines whether the integral converges or diverges.

Let $f(x) = \frac{\cos x - \sin x}{1 + 2\sin(2x)}$. As $x$ approaches $-\frac{\pi}{12}$, the denominator approaches zero. The numerator at this point is:

$\cos(-\frac{\pi}{12}) - \sin(-\frac{\pi}{12}) = \cos(\frac{\pi}{12}) + \sin(\frac{\pi}{12})$

Since $\cos(\frac{\pi}{12}) + \sin(\frac{\pi}{12}) \neq 0$, the integrand has a non-removable singularity at $x = -\frac{\pi}{12}$. This implies the integral diverges.

Therefore, the given integral diverges because of the singularity at $x = -\frac{\pi}{12}$ within the interval of integration.